Théorème de Ménélaus

[Ben314]

[quote="Ben314"]Salut,
De toute façon il n'y a quasiment rien à dire dans cette question, mais de dire "ils sont colinéaires car ils ont la même direction", ça donne un peu l'impression de tourner en rond...

Perso., j'aurais plutôt écrit que, vu que P est (par construction) sur la droite (AB), c'est que A,B et P sont alignés et donc que les vecteurs PA et PB sont colinéaires (ils sont non nuls vu que P est, par construction, distinct de A et de B).

[yann06]

oK
Bonsoir Ben ( merci de m'avoir répondu )
et si a = 1 cela veut dire que les vecteurs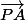 et 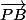sont égaux ?

[yann06]

Bonsoir

3 ) a ) montrer que

b ) En déduire les coordonnées du point M

4 ) a ) Exprimer le vecteur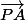 en fonction du vecteur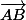

b ) En déduire les coordonnées du point P et montrer que le vecteur a pour coordonnés

[yann06]

pour la 3 )
a ) partant de l'égalité donnée :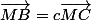 et en introduisant le point A



et donc


soit

il me reste à faire passer le de l'autre coté, et à factoriser





soit

[yann06]

Pouvez m'aidez à trouver le vecteur AM ?

[yann06]

Bonjour

Quelqu'un pour m'aidez à trouver le vecteur AM ?
s'il vous plait

[Lostounet]

Bonjour

Quelqu'un pour m'aidez à trouver le vecteur AM ?
s'il vous plait

Salut
N'as tu pas déjà trouvé AM dans le post précèdent?

[yann06]

Salut

Je viens de voir ton message seulement maintenant ( j'aurais du te répondre bien avant !! )

j'avais trouvé

et pour trouver AM : je dois prendre sont opposé l'opposé de MA )

c'est à dire

Voilà...

[Lostounet]

Attention ce n'est pas comme ça qu'on prend l'opposé.

[yann06]

Salut Lostounet
( comment vas - tu ? )

Peux tu m'expliquer ? s'il te plait

[yann06]

il y a aussi une belle faute d'orthographe : j'ai écrit sont opposé

[Lostounet]

Salut Yann ça va et toi?
Je bosse mes partiels!

Si tu as:


Cela signifie que:

Maintenant pour avoir le vecteur il suffit de multiplier l'égalité précédente par (-1).
Cela donne:




Par distributivité:



À droite (-1)×(-1)/(1-c)=1/(1-c)

Et plus à droite, (-1)×(c/(1-c))= -c/(1-c)

Ce qui signifie

[yann06]

salut Lostounet

j'espère que tu passes un bel après - midi !

c'est quoi les partiels ?

[Lostounet]

C'est les examens de mi-année... ma dernière avant d'avoir un premier diplôme en maths (après la Licence)

[yann06]

chouette !

[yann06]

pour avoir les coordonnées du point P

si on se place dans un repère alors

donc les coordonnées de vecteur sont pour l'abscisse
et pour l'ordonnée

est ce que mon raisonnement est correct ?

[Lostounet]

Oui mais ce sont les coordonnées de M ...