Théorème de Ménélaus
77 messages
- Page 3 sur 4 - 1, 2, 3, 4
Re: théorème de Ménélaus
Tu sais que PA=PB... donc les deux vecteurs ont des coordonnées égales.
Tu peux déduire les coordonnées de P en posant deux équations
Tu peux déduire les coordonnées de P en posant deux équations
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: théorème de Ménélaus
Oui mais ces vecteurs ne sont pas totalement inconnus.
On sait que PB(xB-xP;yB-yP) avec XB et YB connus!
On sait que PB(xB-xP;yB-yP) avec XB et YB connus!
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: théorème de Ménélaus
Et donc.. on a deux équations à examiner.
Bonne nuit
Bonne nuit
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Bonsoir Lostounet
on a tourner en rond autour de questions/réponses complètement hors sujet
en fait c'était beaucoup plus simple
-----------------------------------------------------
On considère un triangle ABC
M,N et P sont trois points situés respectivement sur les droites ( BC ) ( CA ) et ( AB ) distincts des points A,BetC
on cherche à déterminer une condition nécessaire et suffisante d'alignements des points M,N et P
) et
et )
1 ) Justifier l'existence d'un réel a tel que , d'un réel b tel que
, d'un réel b tel que  et un réel c tel que
et un réel c tel que 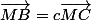
2 ) Justifier que a,b et c sont différents de 1
3 ) a) démontrer que
-------------------------------------------
on a tourner en rond autour de questions/réponses complètement hors sujet
en fait c'était beaucoup plus simple
-----------------------------------------------------
On considère un triangle ABC
M,N et P sont trois points situés respectivement sur les droites ( BC ) ( CA ) et ( AB ) distincts des points A,BetC
on cherche à déterminer une condition nécessaire et suffisante d'alignements des points M,N et P
1 ) Justifier l'existence d'un réel a tel que
2 ) Justifier que a,b et c sont différents de 1
3 ) a) démontrer que
-------------------------------------------
Re: théorème de Ménélaus
Pour la 1 )
les vecteurs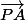 et
et 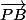 sont colinéaires : il existe un réel a tel que
sont colinéaires : il existe un réel a tel que 
les vecteurs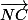 et
et 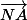 étant colinéaires : il existe un réel b tel que
étant colinéaires : il existe un réel b tel que 
les vecteurs
les vecteurs
Re: théorème de Ménélaus
Bonjour
Les vecteurs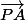 et
et 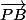 sont colinéaires
sont colinéaires
et les vecteurs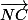 et
et 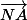 sont également colinéaires
sont également colinéaires
Pour les vecteurs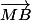 et
et 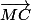
là je ne vois pas comment démontrer l'existence d'un réel c tel que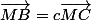
Les vecteurs
et les vecteurs
Pour les vecteurs
là je ne vois pas comment démontrer l'existence d'un réel c tel que
Re:
yann06 a écrit:Bonsoir Lostounet
on a tourner en rond autour de questions/réponses complètement hors sujet
2 ) Justifier que a,b et c sont différents de 1
-------------------------------------------
Je ne pense pas qu'on a tourné en rond on est en train de répondre à 2)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: théorème de Ménélaus
Pour que deux vecteurs 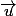 et
et 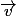 soient colinéaires : il faut un nombre réel k tel que
soient colinéaires : il faut un nombre réel k tel que 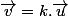
Re: théorème de Ménélaus
Bonsoir
Pour la question 1 )
les deux vecteurs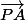 et
et 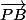 sont colinéaires s'il existe un réel a tel que
sont colinéaires s'il existe un réel a tel que 
donc je peux justifier l'existence de ce réel a si les vecteurs sont colinéaires
le seul fait qu'ils soient qu'ils aient la même direction est suffisant pour dire qu'ils sont colinéaires ?
Quelqu'un pour m'aider ?
Pour la question 1 )
les deux vecteurs
donc je peux justifier l'existence de ce réel a si les vecteurs sont colinéaires
le seul fait qu'ils soient qu'ils aient la même direction est suffisant pour dire qu'ils sont colinéaires ?
Quelqu'un pour m'aider ?
Re: théorème de Ménélaus
Salut,
De toute façon il n'y a quasiment rien à dire dans cette question, mais de dire "ils sont colinéaires car ils ont la même direction", ça donne un peu l'impression de tourner en rond...
Perso., j'aurais écrit que, vu que P est (par construction) sur la droite (AB), c'est que A,B et P sont alignés et donc que les vecteurs PA et PB sont colinéaires (ils sont non nuls vu que P est supposé être différent de A et de B).
De toute façon il n'y a quasiment rien à dire dans cette question, mais de dire "ils sont colinéaires car ils ont la même direction", ça donne un peu l'impression de tourner en rond...
Perso., j'aurais écrit que, vu que P est (par construction) sur la droite (AB), c'est que A,B et P sont alignés et donc que les vecteurs PA et PB sont colinéaires (ils sont non nuls vu que P est supposé être différent de A et de B).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
77 messages
- Page 3 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
