Théorème de Ménélaus
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Nov 2017, 01:18
par Lostounet » 12 Nov 2017, 01:18
yann06 a écrit:A est l'origine du repère donc A (0,0)
B (0,1)
C ( 0,1)
Tu es sûr?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Nov 2017, 01:21
par Lostounet » 12 Nov 2017, 01:21
Je ne vais par contre pas tarder à y aller désolé.
Je me lève tôt pour réviser..moi aussi j'ai un examen de maths Lundi...assez difficile. Il faut sauver les meubles

Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 12 Nov 2017, 01:30
par yann06 » 12 Nov 2017, 01:30
oK c'est sympa de m'avoir aidé
C (0,1)
ça n'est pas cela ?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Nov 2017, 01:31
par Lostounet » 12 Nov 2017, 01:31
Non.
C est sur quel axe ? Abscisses ou ordonnèes?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Nov 2017, 01:33
par Lostounet » 12 Nov 2017, 01:33
Pardon moi aussi je dèconne il semble.
B(1;0) et C(0;1)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 12 Nov 2017, 01:36
par yann06 » 12 Nov 2017, 01:36
j'ai tracé trois droites qui se coupent en A ,B et C
le point B est vers le bas donc axe des abscisses
et C est donc sur l'axe des ordonnées
c'est oK ?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Nov 2017, 01:37
par Lostounet » 12 Nov 2017, 01:37
Oui mais attention au fait que les points sont placés puis les axes.
Donc maintenant que se passe-t-il quand a=1 et b=1?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 12 Nov 2017, 01:40
par yann06 » 12 Nov 2017, 01:40
si a = 1
x' = kx
et
y' = ky

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Nov 2017, 01:43
par Lostounet » 12 Nov 2017, 01:43
Mais ici..? Il faut que tu appliques ces formules. Elles sont vraies.
Seules, ces formules ne signifient rien. Il faut que tu les adaptes à ton exercice
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 12 Nov 2017, 01:46
par yann06 » 12 Nov 2017, 01:46
quand a = 1
les vecteurs
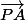
et
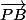
sont colinéaires et égaux ( avec la meme longueur

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Nov 2017, 01:49
par Lostounet » 12 Nov 2017, 01:49
Oui... est-ce possible?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 12 Nov 2017, 01:56
par yann06 » 12 Nov 2017, 01:56
pour calculer les coordonnées de P
je dois d'abord calculer les coordonnées du vecteur AB

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Nov 2017, 01:57
par Lostounet » 12 Nov 2017, 01:57
Oui...
Mais AB a des coordonnées faciles à calculer.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 12 Nov 2017, 02:02
par yann06 » 12 Nov 2017, 02:02
coordonnées du vecteur AB

=

=


-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Nov 2017, 02:04
par Lostounet » 12 Nov 2017, 02:04
Oui
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 12 Nov 2017, 02:09
par yann06 » 12 Nov 2017, 02:09
et si a = 1 les vecteurs sont égaux
dans ce cas


-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Nov 2017, 02:10
par Lostounet » 12 Nov 2017, 02:10
D'où cela sort-il?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 12 Nov 2017, 02:11
par yann06 » 12 Nov 2017, 02:11
si a = 1 les vecteurs sont colinéaires ?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 12 Nov 2017, 02:13
par Lostounet » 12 Nov 2017, 02:13
Oui..et?
Que sont lea coordonnées de P?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
yann06
- Membre Relatif
- Messages: 256
- Enregistré le: 08 Aoû 2016, 10:16
-
 par yann06 » 12 Nov 2017, 02:14
par yann06 » 12 Nov 2017, 02:14
je vois pas comment calculer les coordonnées de P
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités