Théorème de la médiane

[jeremy83]

Salut tout le monde, j'aurais besoin de votre aide,

Voici l'énoncé :

Construire un cercle (C) de centre O, de rayon 8.
Placer un point fixe A tel que OA = 5.
Construire un triangle APQ rectangle et isocèle en A tel que AP = 20.
E et F sont les points d'intersection de [AP] et [AQ] sur (C).
M milieu de [EF].

1. En utilisant le théorème de la médiane dans le triangle OEF, montrer que le point M est caractérisé par l'égalité : OM² +AM² = 64.

-> Je bloque car il me manque la longueur EF et je ne sais comment la calculez :mur: !

2. Déterminer alors l'ensemble des points M cherché.

-> Aucune idée !

Merci à vous tous

[Ericovitchi]

il faut se rappeler ce qu'est le théorème de la médiane :
Par exemple dans le triangle AEF, puisque AM est une médiane ça s'écrit :

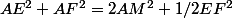
Tu peux dire aussi OM est médiane de OEF et donc que


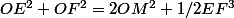
Après c'est assez facile, tu connais OE et OF (qui sont des rayons du cercle et qui valent 8)
Et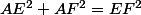 car le triangle est rectangle en A (Pythagore). Tu élimines EF entre les deux équations et il ne te reste plus que des OM et AM et on tombe sur la relation à démontrer.

[Ericovitchi]

pour la suite, encore le théorème de la médiane :
tu prends un point O' milieu de OA et tu transformes en fonction de OO' et MO'
Comme OO' est constant (2,5) et que
alors tu vas trouver une longueur constante pour O'M et donc M parcours un cercle de centre O'

[jeremy83]

Je n'ai toujours pas compris ...

Dans le triangle OEF, M est le milieu de [EF] on a d'après le théorème de la médiane :

OE² + OF² = 2OM² + 1/2EF²

Ensuite comme tu as très bien dit il suffit de remplacer par des valeurs numériques ... Donc :*

<=> 8² + 8² = 2OM² + 1/2EF²
<=> 64 + 64 = 2OM² + 1/2EF²
<=> 128 = 2OM² + 1/2EF²

Et là que faire, je ne comprend plus rien ! Merci pour votre aide :)

[Ericovitchi]

Ca te fait une première équation
mais tu n'as pas utilisé la seconde équation que je t'ai donnée :

à cause du théorème de pythagore
donc et donc en simplifiant

tu remplaces par dans l'équation que tu as trouvée :
et donc

[jeremy83]

EF² = 2AM² + EF²/2 jusqu'à là j'ai compris ensuite tu me dis de simplifier mais il passe où le EF² ?

[Ericovitchi]

Laborieux tout ça :
--> je passe le de l'autre coté

une carotte - 1/2 carotte = 1/2 carotte

[jeremy83]

Oui c'est bon finalement j'avais compris ! Merci beaucoup de ton aide ! J'ai un second exercice qui lui me pose quelques problèmes ! Si tu veux bien m'aider dis le moi ! Je te mettrais l'énoncé :P Merci d'avances

[jeremy83]

Et pour le 2 ? Comment faire je n'ai pas compris ton explication :S

[Ericovitchi]

Je t'avais déjà donné la méthode. Si tu n'essayes pas un minimum par toi même tu ne progresseras pas.
tu prends un point O' milieu de OA et tu transformes en fonction de OO' et MO' grâce toujours au théorème de la médiane :


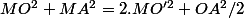
Comme OA est constant (5) et que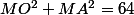
alors tu vas trouver une longueur constante pour O'M et donc M parcours un cercle de centre O'