Théorème de Gauss

par **Elnorth** » 09 Nov 2005, 18:37

Bonjour,

En mathématiques spé, nous sommes en train de voir le théorème de Gauss. Le professeur nous a demandé de faire un exercice pour demain (afin d'avancer le cours), mais je ne comprend pas du tout la démarche à suivre. J'ai tenté de suivre le livre, mais rien de concret n'est disponible.

Voici l'énoncé :
Résoudre dans Z² les équations suivantes :

a) 15x = 48y
(de tête, on trouve facilement x = y = 0, mais il doit y avoir d'autres solutions)

b) 40(x-1) = 25(y+3)

Il me faut uniquement la démarche à suivre. Si vous pouviez prendre appuis sur le a), que je puisse au moins comprendre le raisonnement.

Merci d'avance.

par **boulay59** » 09 Nov 2005, 18:52

a) Déjà, tu peux simplifier ton équation :
5x=16y
Ensuite, on utilise le théorème de Gauss : 5 divise 16y et PGCD(5,16)=1 (ils sont premiers entre eux) donc nécessairement 5 divise y.
Donc il existe a entier relatif tq y=5a
Puis, en réinjectant dans l'égalité de départ, 5x=16*5*a. Donc x=16a

Réciproquement, tous les couples du type (16a, 5a) tq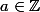

sont solutions.

Donc les solutions sont ...

par **fonfon** » 09 Nov 2005, 18:52

Salut,le theorème de Gauss dit que si:

a divisa bc et si PGCD(a,b)=1 alors a divise c

donc 1) on calcule le PGCD(15,48)=3 donc equation devient 5x=16y

-(x,y) est solution
-(x,y)#(0,0) <=> 5divise18y et 16divise5x
<=> 5divisey et 16divisex car PGCD(5,16)=1 dc Gauss

d'ou les solutions immediates S={(16k,5k) avec k ds Z}

2) on fait pareil

Merci pour mon erreur,je pense qu'il peut utiliser les equivalences la reciproque est immediate

par **boulay59** » 09 Nov 2005, 18:55

Excuse moi fonfon, mais je crois que ton résultat est faux :
ex : x=5*1
y=16*1564879865421548798
D'après toi, c'est une solution !!!!!

N'oublie pas la réciproque et ATTENTION AUX EQUIVALENCES (à éviter au maximum au lycée)

par **Elnorth** » 09 Nov 2005, 19:05

J'ai vraiment rien compris :/
Je dois être bête ... bon, miam time, je verrai ça de nouveau en revenant -_-

par **fonfon** » 09 Nov 2005, 19:08

encore merci ,boulay 59,pour mon erreur j'en avait pas fait depuis 1 an.

qu'est ce que tu ne comprends pas ?

par **Elnorth** » 09 Nov 2005, 19:13

L'ensemble du raisonnement. Le texte ne me pose jamais de problème en général, mais après pour l'adapter à un texte c'est toujours un problème. Pour le moment, je vois bien la première partie :

On calcule le pgcd des deux nombres histoire trouver un diviseur commun, on divise par ce diviseur commun, puis on verifie sur les deux nombres sont "premiers". S'ils le sont, on entre dans une phase de simplification.

On suppose que a = by/x. Donc y doit être divisible par x. Après, on recherche lorsque x est divisible par y.

C'est ici que je fais une brasse coulée ... peut être à cause de la réinjection.

par **fonfon** » 09 Nov 2005, 19:39

RE,
On suppose que a divise by et b divise ax cela vient du fait que (c'est du cours).:

on dit que a divise b ds Z s'il existe q ds Z tq b=aq

Donc ici, a div. by ssi il existe x ds Z tq by=ax, de même b div.ax ssi il existe y ds Z tq ax=by.
Apres pour la resolution de ton equation il faut utiliser le theorème de Gauss pour arriver au resultat deja donné.

par **Elnorth** » 09 Nov 2005, 20:01

Je suis encore plus pommé qu'au début -_-.
Là, par contre, je serais incapable d'expliquer pourquoi. Bon, une relecture de tout ceci s'impose.

Merci pour votre aide et votre patience.

par **Elnorth** » 09 Nov 2005, 20:14

J'ai compris la partie la plus importante, donc ça va :)
Merci pour votre aide.

Théorème de Gauss

Théorème de Gauss

Qui est en ligne