Théorème des quatre carrés : démonstration

[lapras]

Bonjour, je suis en seconde, j'aimerais démontrer le théoreme des quatre carrés de lagrange.
Apres avoir démontré l'identité remarquable : (a²+b²+c²+d²)(x²+y²+z²+t²) = (ax + by + cz + dt)² + (ay - bx - ct + dz)² + (az + bt - cx - dy)² + (at - bz + cy - dx²) par un tres long et fastidieux développement... (d'ailleurs je vous demande si c'est la bonne méthode pour démontrer cette identité...), on doit démontrer que, considérant un nombre premier impair p, il existe (a,b) appartenant a Z² tel que p divise 1 + a² + b²

pour cette question j'ai pas beaucoup d'idées, mais j'ai quand meme essayé qqchose :

soit a et b deux nombres pairs, alors a² + b² est pair donc a² + b² + 1 est impair. Si a² + b² +1 est supérieur ou égal à p, alors p peut etre divisible par a² + b² + 1 (la je n'arrive pas a le démontrer, ca me semble logique , exemple : p = 3 , a = 1 , b= 2 : 3 divise 2 + 1² + 1 = 6 )



Voila pour le début de la démonstration , j'ai donc du mal a le faire :s


merci d'avance de votre aide précieuse !

bye

[oscar]

Bonjour Voici une démonstration

http://img508.imageshack.us/img508/2816/theoremedelagrangegn9.jpg

[lapras]

salut,
ce n'est pas une déonstration mais une introduction a la démonstration :(

je ne trouve pas de démo sur le net :(

[yos]

C'est dans tout livre d'arithmétique et c'est pas niveau seconde (ni même term S).
Tu peux essayer de prouver qu'un entier de la forme 8k+7 est pas somme de trois carrés : ça c'est niveau seconde.

[aviateurpilot]

on doit démontrer que, considérant un nombre premier impair p, il existe (a,b) appartenant a Z² tel que p divise 1 + a² + b²

N.B=dans mon resonnmemet et card(E)=le nombre d'element de qui n'on pas la meme congruence modulo

soit un nombre premier
soient
il est clair que
si
alors (imppossible car )
donc
c-a-dire
donc

[lapras]

salut,
merci pour la démo
il me reste deux questions
le cardinale de S est (p + 1)/2 , j'ai essayé sur plein d'exemple ca marche.
mais j'iamerais bien qu'on me le démontre, comment on fait ?

aussi, pour card(E U S) inférieur ou égal à card ( {0,1,2..., p-1) }, comment le démontrer ?

merci d'avance

[aviateurpilot]

pour card(E U S) inférieur ou égal à card ( {0,1,2..., p-1) }
c'est parce card(E U S)= le nopmbre d'element qui ont des congruence different modulo p
mais il n y a que p conguence modulo p se sont {0,1,2..., p-1}
donc card(E U S) inférieur ou égal à p.

pour

or on a


..
..
..

et le cas de
donc
donc

[lapras]

Ok j'ai compris ta démonstration.
j'ai d'autres questions qui suivent pour la démonstration de ce superbe théoreme :
Soit E l'ensemble des entiers naturels n >= 1 tel que np soit somme de quatre carrés d'entiers. Montrer que E n'est pas vide.
on sait que p divise a² + b² + 1²
0 est un entier, 0² est un entier au carré
1 * p = a² + b² + 1² +0² avec n = 1 donc l'ensemble comporte au moins n = 1 , et donc E n'est pas vide.
Ma démonstration tient elle la route, comment le démontrer autrement ?

On note m le plus petit élément de E. Montrer que m
m = 1 car n >= 1
p est impair, meme si p est le plus petit possible, il est au minimum égal à 3, car 3 est le premier nombre premier impair.
don c mOn sait que a² et b² sont des entiers, qu'ils soient pairs ou impairs, a² + b² + 1² est toujours impair, donc le produit mp doit etre impair, or p est pair donc m doit etre pair pour que mp soit impair
donc m est forcément impair.


merci d'avance de me corriger cet essai de démonstraton, qui me semble bien ratée...

bye

[Quidam]

Me revoilà ! Je sais, c'était un peu long, mais d'autres contraintes...
En fait, j'ai essayé deux autres approches, et j'ai perdu pas mal de temps à chercher pour quelle raison les deux résultats conséquents étaient incompatibles...
Enfin, j'ai réussi à obtenir deux résultats qui ne se contredisent pas l'un l'autre...
Voici donc ma deuxième approche !

Dans la figure ci-dessus, je représente une sphère céleste de rayon R. Le repère Oxyz, est défini par AB (Ox), CD (Oy) et NS (Oz). Ce dernier est l'axe de rotation de la Terre sur elle-même. Je représente la trajectoire d'un jeu de quatre satellites, le cercle AHB, le repère ayant été choisi pour que l'axe de cette trajectoire soit dans le plan Oyz (OCNDS). L'axe du satellite est incliné d'un angle 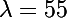degrés ( 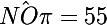degrés). On a vu voir post précédent que pour que l'angle de vue, à partir d'un point de la Terre, d'une trajectoire soit , il fallait que la distance angulaire entre ce point et l'axe de la trajectoire satellite soit de 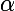, de manière que :

Pour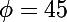 degrés, soit 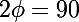degrés, c'est-à-dire, pour que l'on voit toujours au moins un satellite sur une trajectoire donnée, on obtient 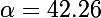degrés. Ceci signifie que tous les points de la Terre situés à une distance angulaire de l'axe supérieure à 42 degrés voient en permance un moins un satellite sur cette orbite.

Voyons ce qui se passe au niveau de l'équateur : les deux cercles bleus, sont les limites de la zone. Tous les points situés entre les deux cercles bleus voient au moins un satellite sur cette orbite. En particulier, au niveau de l'équateur, la zone d'où l'on voit en permanence au moins un satellite est représentée par l'arc EAF sur l'équateur, arc qui représente un angle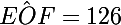 degrés (et aussi autant de l'autre côté !) !
Ainsi, une seule orbite "couvre" deux zones de largeur 126 degrés, soit plus des deux tiers de la totalité de l'équateur. Pour tous les points de cette zone, au total de 252 degrés, on voit en permanence au moins un satellite sur cette orbite. Il suffit alors de faire intervenir les 5 autres orbites - décalées de 60° chacune par rapport à la précédente, pour s'apercevoir que tous les points de l'équateur sont "couverts" par quatre orbites et par conséquent que tous les points de l'équateur "voient" en permanence 4 satellites parmi les 24 objets volants identifiés !
Vu du pôle, j'ai représenté les zones de couverture par six "paires d'arcs de cercle, chacun de longueur 126 degrés", ci-dessous.


Bien sûr, ce n'est pas terminé : il faut voir ce qui se passe à d'autres latitudes, mais au moins, ce résultat n'est plus en désaccord avec ma troisième approche...
Au passage, on notera quand même que les pôles sont inclus dans les zones "d'où l'on voit en permanence un satellite sur cette orbite". Il en résulte que pour ce qui concerne les pôles, il est certain qu'ils voient en permanence 6 satellites. Reste à chercher si d'aventure à certaines latitudes intermédiaires cette belle garantie tient le coup...

[aviateurpilot]

on a pas forcement
1*p=a²+b²+1
on a seulement p|a²+b²+1, c-a-dire, l'existance d'un k tel que kp=a²+b²+1

on a pas forcement m=1.

[aviateurpilot]

car
donc

ou bien comme tu as dit, si on comsidere que 0 est un carré parfait
on a ,donc il existe tel que
d'ou et donc