Théorème des Accroissements Finis =)

[Nightmare]

Alors, un exercice plus difficile sur le TAF et un exercice simple sur les équivalents :

TAF :
Soient a et b deux réels tels que a < b et f une application définie et dérivable sur ]a,b[ telle que

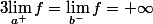
Montrer que

(Tu pourras admettre le théorème de Darboux ou le démontrer si tu le souhaites mais c'est beaucoup plus difficile)

Equivalents :
Donner des équivalents simples de , , et au voisinage de 0.

Pour utiliser les petit o :
Montrer que

[J-R]

si je peux me permettre de revenir à ton exo Nightmare.

on a notre fonction f qui se comporte comme l'expo en +oo.

et donc en fait on veut prouver qu'un équivalent de la dérivée de cette fonction f est encore l'expo (d'où une histoire avec une des propriétés fondamentale de l'expo qui est sa propre dérivée...).

y a t-il pas une propriété qui dit que si alors où un truc du genre ....

si ca demande vraiment des notions je laisse tomber.

par contre des exos sur les dl ou autre exos d'analyse je prend...

[J-R]

ah mais attend en fait quand on nous dit donner un ééquivalent simple de sin(x) en 0 c'estt comme si on nous demandait de trouver un dl en 0 d'ordre 1 de sin(x) ?

[Nightmare]

Oui et non.

Ici oui, mais un DL fourni un équivalent polynômial (à l'ordre 1 en tout cas) mais on peut trouver des équivalents non polynômiaux mais bon c'est rare. (prendre mon premier exercice sur les équivalents posté plus haut, on a une fonction f équivalent à l'exponentielle en +oo, l'exponentielle qui n'est pas polynômiale. D'ailleurs c'est un exercice sympa bien que facile : Montrer qu'il n'existe pas de polynôme P tel que pour tout x, P(x)=exp(x))

:happy3:

[raito123]

Le théorème de Darboux : je ne le connais pas donc je vais faire une petite recherche !!

Pour les équivalences des fonctions que tu m'as donner y a une évidente

J-R : On a pas encore traiter cet exo pasque je sais presque rien sur les équivalences xD:

[J-R]

ok d'accord faut pas que je mélange... merci

Montrer qu'il n'existe pas de polynôme P tel que pour tout x, P(x)=exp(x))

si je montre que toute fonction polynome est négligeable par rapport à l'exponentielle en +oo...

J-R : On a pas encore traiter cet exo pasque je sais presque rien sur les équivalences xD:

moi aussi mais c'est juste pour en toucher 2 mots ...

[Nightmare]

raito > Peux-tu préciser pour l'équivalent ?

J-R > C'est vrai mais il y a beaucoup plus simple.

[raito123]

En fait y a une question : y a une méthode pour trouver les equivalences y-il des propriétés (outils) pour les trouver ou doit-on travailler à tor et à travers? Ou ça vient avec un peu d'entrainement?!!!

[Nightmare]

Là ce sont des équivalents simples donc la seule méthode est la connaissance des limites usuelles.

Par exemple quelle est la limite de sin(x)/x lorsque x tend vers 0? Donc ... ?

[raito123]

Ok!!!

Pour l'exo de nightmare : toute les fonctions que tu m'as donner convergent vers 0 lorsque x tend vers 0 et puisque f(x)=x^n pour n>0 converge vers 0 quand x tend vers 0 alors f est un equivalent !!!!

[Nightmare]

Euh je n'ai pas du tout compris :marteau:

Déjà que veux-tu dire par "f est une équivalence" ? On dit que deux fonctions sont équivalentes ou que f est équivalent à g mais dire "f est une équivalence" n'a pas de sens.

Sinon, en quoi le fait que deux fonctions convergent vers 0 montrent qu'elles sont équivalentes? C'est faux a priori.

Quelle est la définition de l'équivalence que tu as vu sur internet?

[raito123]

la fonction constante f(x)=1 est un equivalent de sin(x)/x au voisinage de 0 !!

e^x est aussi un equivalent de sin(x)/x au voisinage de 0

[Nightmare]

effectivement 1 est équivalente à sin(x)/x en 0 mais bon je te demandais un équivalent de sin(x) et non de sin(x)/x.

Cela dit tu auras compris une chose, une fonction est toujours équivalente à sa limite en un point. Cela dit tu auras compris une autre chose, ce n'est pas utile de savoir ça :lol3:

[raito123]

Euh je n'ai pas du tout compris :marteau:

Déjà que veux-tu dire par "f est une équivalence" ? On dit que deux fonctions sont équivalentes ou que f est équivalent à g mais dire "f est une équivalence" n'a pas de sens.

Sinon, en quoi le fait que deux fonctions convergent vers 0 montrent qu'elles sont équivalentes? C'est faux a priori.

Quelle est la définition de l'équivalence que tu as vu sur internet?

Ah ok!!

J'ai vu que de fonctions sont equivalentes au voisinage de 0 veut dire qu'ils ont le même comportement au voisinage de a !!!

Ok je vois les choses un peu plus claire!!!

Cela dit tu auras compris une chose, une fonction est toujours équivalente à sa limite en un point. Cela dit tu auras compris une autre chose, ce n'est pas utile de savoir ça

Mdr^^

Alors faut savoir quoi au juste !!!?

[Nightmare]

Oui ça c'est ce que je t'ai dit mais c'est une vulgarisation de la définition et ne permet pas de travailler dessus.

Deux fonctions f et g sont équivalentes au voisinage de a ssi il existe une fonction h qui converge vers 1 en a telle que f(x)=h(x)g(x)

[raito123]

Aha,

Donc f(x)=x est un équivalent de sin(x) au voisinage de 0 car :

C'est bon?

[Nightmare]

car sin(x)/x tend vers 1 surtout.

sin(x)=sin(x)/x * x
ie sin(x)=h(x) * x avec h qui tend vers 1 donc on a bien sin(x) et x qui sont équivalentes en 0.

[raito123]

Oui !!

Merci nightmare t'es vraiment sympa !!

Je réfléchirai au autres exos et je posterai ce que je trouve!!!

Mtn je file (j'ai un devoir cette semaine en physique je dois réviser)


A++

[raito123]

Re,

J'ai trouver deux equivalents pour la fonction au voisinage de 0 :

La premiére car et converge vers 1 quand x tend vers 0 !!

La deuxiéme

Efféctivement on peut trouver beaucoup d'autre!!!

[Nightmare]

effectivement exp(x)-1 est équivalent à x.

le reste je n'ai pas compris...