Théorème des Accroissements Finis =)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 09 Mar 2008, 21:41
par raito123 » 09 Mar 2008, 21:41
En gardant les même notations de mon dernier post :
=g(x)\frac{sin(x)}x)
et puisque sinx/x converge vers 1 quand x tend vers 0 alors g et et K sont equivalents !!
C'est bon?
Les multiples ne doivent pas être utilisés sans nécessité
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 09 Mar 2008, 21:43
par Nightmare » 09 Mar 2008, 21:43
Oui mais bon ce n'est pas vraiment un équivalent simple, tu le compliques plus qu'autre chose là !

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 09 Mar 2008, 21:45
par raito123 » 09 Mar 2008, 21:45
Ah ok!!!
Il n'est pas simple mais il est un equivalent ?
Les multiples ne doivent pas être utilisés sans nécessité

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 12 Mar 2008, 00:06
par raito123 » 12 Mar 2008, 00:06
Re,
f(x) et g(x) sont equivalents au voisinage de 0 avec :
=1-cos(x))
et
=\frac{x^2}2)
Les multiples ne doivent pas être utilisés sans nécessité
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Mar 2008, 00:08
par Nightmare » 12 Mar 2008, 00:08
c'est bon :happy3:
Pour éviter d'avoir à faire une phrase tu peux écrire
\sim \frac{x^{2}}{2})
(commande LaTeX : \sim)

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 12 Mar 2008, 00:12
par raito123 » 12 Mar 2008, 00:12
Ok merci :we:
Mtn ça chauffe pour les deux autres exos !!
Les multiples ne doivent pas être utilisés sans nécessité
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 27 Mar 2008, 19:59
par J-R » 27 Mar 2008, 19:59
allez comme promis:
Montrer que :

^x<e<(\frac{1+x}{x})^{x+1}}})

-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 27 Mar 2008, 20:09
par _-Gaara-_ » 27 Mar 2008, 20:09
Yeah !
Mercii je vais le faire tout de suite :P
Je laisse l'anglais en PAUSE ^^

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 27 Mar 2008, 20:15
par raito123 » 27 Mar 2008, 20:15
J-R a écrit:allez comme promis:
Montrer que :

^x<e<(\frac{1+x}{x})^{x+1}}})

TAF ? :ptdr:
Les multiples ne doivent pas être utilisés sans nécessité
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 27 Mar 2008, 20:27
par _-Gaara-_ » 27 Mar 2008, 20:27
raito123 a écrit:TAF ? :ptdr:
wai héhé :id:
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 27 Mar 2008, 20:28
par J-R » 27 Mar 2008, 20:28
c'est à dire que notre ami gaaras s'ennuyait devant son dm d'anglais. Ainsi il me demanda un petit divertissement et donc en effet c'est un cadeau avec le taf...
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 27 Mar 2008, 20:31
par Babe » 27 Mar 2008, 20:31
peut on uilisé le fait que
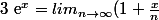^n)
mais jsuis pas sur
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 27 Mar 2008, 20:34
par _-Gaara-_ » 27 Mar 2008, 20:34
J-R a écrit:c'est à dire que notre ami gaaras s'ennuyait devant son dm d'anglais. Ainsi il me demanda un petit divertissement et donc en effet c'est un cadeau avec le taf...
héhé !! en effet ! ce DM d'anglais est long, compliqué, incompréhensible etc.. alors que les maths c'est convivial =)
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 27 Mar 2008, 20:34
par _-Gaara-_ » 27 Mar 2008, 20:34
Babe a écrit:peut on uilisé le fait que
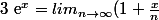^n)
mais jsuis pas sur
C'est ce que je me suis dit au début mais j'ai rien trouvé

-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 27 Mar 2008, 20:36
par J-R » 27 Mar 2008, 20:36
babe : vas y lance toi toute solution est bonne à prendre (bon j'ai pas fait comme ca mais bon ...)
indice pour gaaras (et les autres): montrer que ceci est équivalent à :
-ln(x))<1<(x+1)(ln(x+1)-ln(x))})
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 27 Mar 2008, 21:16
par lapras » 27 Mar 2008, 21:16
[quote="J-R"]allez comme promis:
Montrer que :

[TEX]4$\blue{\fbox{(\frac{1+x}{x})^x
x*(ln(x+1) - ln(x))
1/x > ln(x+1) - ln(x) => x*(ln(x+1) - ln(x)) < 1
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 27 Mar 2008, 21:22
par _-Gaara-_ » 27 Mar 2008, 21:22
Salut lapras,
j'ai fait pareil que toi mais je ne sais pas si c'est suffisant >.<
Tu crois que c'est bon comme çà ?? :++:
=)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 27 Mar 2008, 21:26
par lapras » 27 Mar 2008, 21:26
bah oui
c'est une application du TAF sur [x ; x+1] avec la fonction ln
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 27 Mar 2008, 21:29
par _-Gaara-_ » 27 Mar 2008, 21:29
lapras a écrit:bah oui
c'est une application du TAF sur [x ; x+1] avec la fonction ln
Ok donc, comme d'hab je cherchais minuit à ln(heure) xD
Bien joué =)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 27 Mar 2008, 21:31
par lapras » 27 Mar 2008, 21:31
en fait je viens de découvrir le TAF y'a 5 min (enfin je veux dire je viens de le découvrir + le démontrer donc démontrer le théoreme de Rolle)
C'est assez intuitif et c'est surprenant ce qu'on peut faire avec !
:we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
