TermS : tangente et signe d'une fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
hpauline
- Membre Naturel
- Messages: 35
- Enregistré le: 06 Oct 2007, 14:21
-
 par hpauline » 23 Nov 2008, 14:21
par hpauline » 23 Nov 2008, 14:21
bonjour,
 = (1+x)^n)
on me demande de terminer la tangente T de f (d'équation g) en O et j'ai obtenu
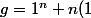^{n-1} x)
cela vous semble juste ?
je dois étudier ensuite le signe de f-g
je ne sais pas si l'équation de laquelle je pars est bonne ni comment étudier le signe puisqu'il y a 2 inconnues : x et n
merci de votre aide
-
phibre75
- Messages: 3
- Enregistré le: 23 Nov 2008, 13:26
-
 par phibre75 » 23 Nov 2008, 14:27
par phibre75 » 23 Nov 2008, 14:27
bonjour
manifestement ça ne fonctionne pas:
ta tangente touche ta courbe au point d'absciise 0
or pour chacune de tes fonctions fn, fn(0) = 1 et tes gn(0) ne valent pas 1.
utilse correctement ta formule g(x) = f ' (0) (x-0) + f( 0)
en calculant au préalable f ' (x) ( f est de la forme ...... )
pour étudier la position de f et g tu réecriras f-g et en l'appelant h tu étudieras les variations de h...
-
johnjohnjohn
- Membre Rationnel
- Messages: 843
- Enregistré le: 24 Oct 2006, 11:00
-
 par johnjohnjohn » 23 Nov 2008, 14:37
par johnjohnjohn » 23 Nov 2008, 14:37
hpauline a écrit:bonjour,
 = (1+x)^n)
on me demande de terminer la tangente T de f (d'équation g) en O et j'ai obtenu
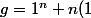^{n-1} x)
cela vous semble juste ?
je dois étudier ensuite le signe de f-g
je ne sais pas si l'équation de laquelle je pars est bonne ni comment étudier le signe puisqu'il y a 2 inconnues : x et n
merci de votre aide
Ton équation de droite est juste. Néanmoins, tu peux peut-être l'expliciter de façon moins lourdingue.
En effet soit p un entier, alors 1^p=1.
ça devrait t'aider à y voir clair dans l'expression de f-g
-
hpauline
- Membre Naturel
- Messages: 35
- Enregistré le: 06 Oct 2007, 14:21
-
 par hpauline » 23 Nov 2008, 15:34
par hpauline » 23 Nov 2008, 15:34
merci , c'est déjà mieux !
j'obtiens :
^n - (1+nx))
est-ce utile et possible de développer la fonction obtenue ?
en effet , je dois ensuite étudier les variations de f-g ;
je calcule les dérivées et j'ai alors :
= n (1+x)^{n-1})
= n)
d'où
' (x) = n(1+x)^{n-1} - n)
je ne vois pas comment en déduire le tableau de variation , il y a 2 inconnues... pourriez-vous m'aider ?
-
hpauline
- Membre Naturel
- Messages: 35
- Enregistré le: 06 Oct 2007, 14:21
-
 par hpauline » 23 Nov 2008, 17:44
par hpauline » 23 Nov 2008, 17:44
une idée svp ? je suis bloquée pour la suite de l'exercice...
-
johnjohnjohn
- Membre Rationnel
- Messages: 843
- Enregistré le: 24 Oct 2006, 11:00
-
 par johnjohnjohn » 23 Nov 2008, 18:41
par johnjohnjohn » 23 Nov 2008, 18:41
hpauline a écrit:d'où
' (x) = n(1+x)^{n-1} - n)
?
Tu pourrais poser h=(f-g)' et étudier les variations de h. ( dérivée, tableau de variations, limites , ... )
Si tu arrives à déterminer le signe de h sur son intervalle d'étude, ça devrait répondre à la question
-
hpauline
- Membre Naturel
- Messages: 35
- Enregistré le: 06 Oct 2007, 14:21
-
 par hpauline » 23 Nov 2008, 20:51
par hpauline » 23 Nov 2008, 20:51
l'ennui est qu'il y a 2 inconnues... je peux faire quoi pour me débloquer?
-
johnjohnjohn
- Membre Rationnel
- Messages: 843
- Enregistré le: 24 Oct 2006, 11:00
-
 par johnjohnjohn » 23 Nov 2008, 21:47
par johnjohnjohn » 23 Nov 2008, 21:47
hpauline a écrit:l'ennui est qu'il y a 2 inconnues... je peux faire quoi pour me débloquer?
On ne te demande pas de résoudre une équation mais d'étudier une fonction. Il faut considérer x comme une variable et n un paramètre de la fonction de variable x.
Tu devrais donc étudier la fonction h que je t'ai posée.
1) dérivée de h
2) tableau de variation de h
3) limites de h
4) signe de h
il faudra peut-être distinguer plusieurs cas selon les valeurs de n
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
