Terminale ES- Identification coefficient, avis aux experts
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Cedrick0910
- Messages: 5
- Enregistré le: 18 Nov 2010, 19:48
-
 par Cedrick0910 » 18 Nov 2010, 19:53
par Cedrick0910 » 18 Nov 2010, 19:53
Bonsoir à tous,
j'ai un problème sur un exercice de maths que je n'arrive, malgré mes sincères efforts, pas à résoudre.
Voici l'énoncé :
On considère une fonction f définie sur ]3;+infini[ :
f(x) = 9X / (x² - 9 )
1/ Première question :
Déterminer les réels a et b tels que sur ]3; +infini[ :
f(x) = [a / (x-3)] + [b / (x+3)]
J'ai bien essayé toutes les techniques, je n'y arrive vraiment pas.
Pourriez-vous m'aider sil-vous-plait ?
Merci d'avance
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Nov 2010, 20:04
par Dinozzo13 » 18 Nov 2010, 20:04
Salut !
Met
 = \frac{a}{x-3}+\frac{b}{x+3})
au même dénominateur.
-
Cedrick0910
- Messages: 5
- Enregistré le: 18 Nov 2010, 19:48
-
 par Cedrick0910 » 18 Nov 2010, 20:13
par Cedrick0910 » 18 Nov 2010, 20:13
Merci de ta vive réponse ! :)
Je l'avais fait pourtant :(
f(x) = a(x+3) + b(x-3) / (x²+9)
f(x) = (ax+bx+3a-3b) / (x²+9) = 9x/ (x²-9)
d'où ax+bx+3a-3b = 9x....
et ensuite me voilà bloqué.
-
Anonyme
 par Anonyme » 18 Nov 2010, 20:29
par Anonyme » 18 Nov 2010, 20:29
Je vais sûrement dire une bêtise ...
Je pense qu'il faut developper ton expression pour arriver à la forme donnée,
De là tu peux identifier :lol3:
-
Cedrick0910
- Messages: 5
- Enregistré le: 18 Nov 2010, 19:48
-
 par Cedrick0910 » 18 Nov 2010, 20:35
par Cedrick0910 » 18 Nov 2010, 20:35
Développer 9x / x²+9 ?
-
Anonyme
 par Anonyme » 18 Nov 2010, 20:43
par Anonyme » 18 Nov 2010, 20:43
Je pense :)
Après il faut que tu arrives à f(x) = [a / (x-3)] + [b / (x+3)],
Mais je ne suis pas sûr du tout :scotch:
-
Cedrick0910
- Messages: 5
- Enregistré le: 18 Nov 2010, 19:48
-
 par Cedrick0910 » 18 Nov 2010, 20:50
par Cedrick0910 » 18 Nov 2010, 20:50
Hum... ça revient donc au même.
Mais je crois que le problème est sur l'ensemble de définition...
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 18 Nov 2010, 20:54
par Dinozzo13 » 18 Nov 2010, 20:54
il s'agit d'effectuer une identification :
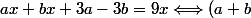x+3(a-b)=9x)
Or tu sais que deux polynômes sont égaux ssi leurs coefficients sont respectivement égaux. Par identification, cela équivaut à :
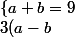=0)
-
Cedrick0910
- Messages: 5
- Enregistré le: 18 Nov 2010, 19:48
-
 par Cedrick0910 » 18 Nov 2010, 21:08
par Cedrick0910 » 18 Nov 2010, 21:08
Voilà un théorème que j'avais oublié ...
Je te remercie beaucoup de ton aide,
j'ai réussi à finir mon exercice.
Encore merci,
bonne soirée !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
