Terme générale d'une suite

[Tombri]

Bonjour,

j'aurai besoin d'aide svp : quelle est l'expression du terme général d'une suite de la forme :



Avec a élément de Z

Merci

[Sourire_banane]

Salut,

Quel est le premier terme de la suite ?

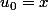
Si , , , , etc.

[Tombri]

Salut,

Quel est le premier terme de la suite ?

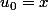
Si , , , , etc.

Merci de ta réponse ! Uo est un entier naturel ! En fait je me demandais si il était possible de trouver une expression (quelle que soit la suite) de la suite U au rang p en fonction de n ! Lorsque j'essaye pour une suite telle que (4Un + 3^Un +1)/4 par exemple, je bloque a cause du 3^Un

[Sourire_banane]

Cette suite a quand même l'air d'avoir un comportement très très vif.

[Tombri]

Cette suite a quand même l'air d'avoir un comportement très très vif.

Que veux-tu dire par vif ? Qui augmente croîts rapidement ? Oui j'en suis conscient mais donc tu ne connais pas la méthode pour résoudre mon problème ?

[paquito]

Commençons par exclure aa^x n'est définie que pour a>0, excluons le cas a=1, sans intérêt et commençons par U0=1;
U1=a, U2=a^a, U3=a^a^a=a^(a²), U4=a^a^(a²)=a^(a^3), ...., Un=a^(a^(n-1)), récurrence évidente.
a^(n-1) est une suite géométrique, donc:

si a>1, a^(n-1)->+inf et Un->+inf (ln(Un)=(a^(n-1))ln(a)).

Si 00 et donc Un->1.

Si U0 est un entier naturel>0, U1=a^U0, U2=a^a^UO=a^(aU0),U3=a^a^(aU0)=a^(a²Uo), donc ça ne change rien (Un=a^(U0.a^(n-1)).

[Tombri]

Commençons par exclure aa^x n'est définie que pour a>0, excluons le cas a=1, sans intérêt et commençons par U0=1;
U1=a, U2=a^a, U3=a^a^a=a^(a²), U4=a^a^(a²)=a^(a^3), ...., Un=a^(a^(n-1)), récurrence évidente.
a^(n-1) est une suite géométrique, donc:

si a>1, a^(n-1)->+inf et Un->+inf (ln(Un)=(a^(n-1))ln(a)).

Si 00 et donc Un->1.

Si U0 est un entier naturel>0, U1=a^U0, U2=a^a^UO=a^(aU0),U3=a^a^(aU0)=a^(a²Uo), donc ça ne change rien (Un=a^(U0.a^(n-1)).

Merci ! Tu as été très clair