Oui oui, je vois bien maintenant ....
Moi je me suis fait avoir, j'ai calculé la limite .. même pas réfléchis.
[Défi****] Term C - Intégration
33 messages
- Page 2 sur 2 - 1, 2
par ned aero » 03 Avr 2010, 14:40
Merci pour vos commentaires, je réapprends beaucoup...
j'avais raisonné comme ffpower. la solution de Ben314 est élégante mais un élève passant le bac n'osera peut être pas, évitera tout risque en calculant la limite ou laissera tomber...donc j'ai fais comme Benekire
problème éludé lors de la conception de l'exercice? peut-être...
salut à vous
j'avais raisonné comme ffpower. la solution de Ben314 est élégante mais un élève passant le bac n'osera peut être pas, évitera tout risque en calculant la limite ou laissera tomber...donc j'ai fais comme Benekire
problème éludé lors de la conception de l'exercice? peut-être...
salut à vous
par Dinozzo13 » 03 Avr 2010, 16:51
Salut !
Me revoilà pour vous donner l'avant dernière partie de cet exercice :
B.1°)a)+iS_n(t)=q+q^2+...+q^n)
en posant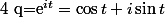 
.
(Utiliser la relation de Moivre)
Si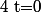
alors 
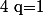et =n+1)
Si
alors iS_n(t)=q\frac{1-q^n}{1-q})
iS_n(t)=e^{it}\frac{1-e^{nit}}{1-e^{it}}=e^{it} \frac{ e^{i\frac{nt}{2}}\left( e^{i\frac{nt}{2}}-e^{-i\frac{nt}{2}} \right) }{ e^{i\frac{t}{2}} \left (e^{i\frac{t}{2}}-e^{-i\frac{t}{2}} \right) })
.
iS_n(t)=e^{i\frac{(n+1)t}{2}} \frac{\sin \frac{nt}{2}}{\sin \frac{t}{2}})
.
Et enfin, prendre la partie réelle de+iS_n(t))
pour conclure.
b) En effet, la seule difficulté ici, est de montrer la continuité en zéro.
En fait, tout ce qu'il faut faire c'est écrire :
sous la forme 
.
et utiliser le fait que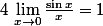
.
2°) Penser à la relation trigonométrique :
=\sin a \cos b + \sin b \cos a)
.
En ce qui concerne le prolongement par continuité, poser g_n(0)=2n+1 et utiliser toujours la même relation ^^ :.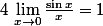
3°) ici, il faut faire une intégration par parties deux fois de suite.
Utiliser la linéarité de l'intégrale.
 C_n(t) \quad dt = \int_0^\pi \left( \frac{t^2}{2\pi} - t \right) \sum_{k=1}^n \cos kt \quad dt = \sum_{k=1}^n \frac{1}{k^2} = u_n)
.
 (1+2C_n(t)) \quad dt =\frac{1}{2} \int_0^\pi \left( t-\frac{t^2}{2\pi} \right) g_n(t) \quad dt)
.
Et voilà, je posterai soit ce soir, soit demain, la dernière partie ^^.
Bonne fin de soirée :++:
Me revoilà pour vous donner l'avant dernière partie de cet exercice :
B.1°)a)
(Utiliser la relation de Moivre)
Si
Si
Et enfin, prendre la partie réelle de
b) En effet, la seule difficulté ici, est de montrer la continuité en zéro.
En fait, tout ce qu'il faut faire c'est écrire :
et utiliser le fait que
2°) Penser à la relation trigonométrique :
En ce qui concerne le prolongement par continuité, poser g_n(0)=2n+1 et utiliser toujours la même relation ^^ :
3°) ici, il faut faire une intégration par parties deux fois de suite.
Utiliser la linéarité de l'intégrale.
Et voilà, je posterai soit ce soir, soit demain, la dernière partie ^^.
Bonne fin de soirée :++:
par benekire2 » 03 Avr 2010, 17:25
on pourra inclure la remarque de ben , pour la continuité de 2Cn+1 !!
par Dinozzo13 » 05 Avr 2010, 23:24
Salut ! :+++:
Le week-end était tellement long que j'ai failli oublié de donner la dernière partie ^^.
Partie C
1°) Pour
, 
se représente comme quotient de deux fonctions continues, est donc continue sur 
.
Continuité en zéro :
 = \lim_{t\to 0} \frac{2\left(1- \frac{t}{2\pi}\right)}{\frac{\sin \frac{t}{2}}{\frac{t}{2}}}=2=f(0))
Puisque
.
La fonction
est positive sur 
et \ge 0)
pour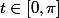 
.
La fonction est donc positive sur 
D'autre part, est continue sur ce segment. est par suite, bornée sur
2°)a) Utiliser le fait que la fonction sinus est bornée par 1.
2°)b) est dérivable sur 
en tant que quotient de deux fonctions dérivables.
=\frac{ \left(1- \frac{t}{\pi}\right)\sin \frac{t}{2}-\frac{1}{2}\left(t-\frac{t^2}{2\pi}\right)\cos\frac{t}{2} }{\sin^2 \left(\frac{t}{2}\right)})
.
f' est continue sur en tant que quotient de fonctions continues. Il s'ensuit que 
est bornée sur ce segment.
2°)c) \frac{\cos \frac{2n+1}{2}t}{\frac{2n+1}{2}}\right]_{\alpha}^{\pi}+\frac{2}{2n+1} \int_{\alpha}^{\pi} f'(t)\cos \frac{2n+1}{2}t \quad dt)
.
Utiliser le fait que
et 
pour conclure.
3°) La relation de Chasles permet d'écrire :
 \sin \frac{2n+1}{2}t \quad dt + \frac{1}{2}I_n)
D'où :
 \sin \frac{2n+1}{2}t \quad dt\right| + \frac{1}{2}\left| I_n \right|)
Le premier membre de cette inégalité converge, puisque u converge. Il s'ensuit que :
.
Cette dernière inégalité est vraie pour tout
.
Conclure :=\frac{\pi^2}{6})
.
Et voilà, @+
Le week-end était tellement long que j'ai failli oublié de donner la dernière partie ^^.
Partie C
1°) Pour
Continuité en zéro :
Puisque
La fonction
La fonction
2°)a) Utiliser le fait que la fonction sinus est bornée par 1.
2°)b)
f' est continue sur
2°)c)
Utiliser le fait que
3°) La relation de Chasles permet d'écrire :
D'où :
Le premier membre de cette inégalité converge, puisque u converge. Il s'ensuit que :
Cette dernière inégalité est vraie pour tout
Conclure :
Et voilà, @+
par Dinozzo13 » 22 Juin 2010, 14:02
Salut !
En reprenant cet exo, je viens de remarquer que j'ai peut-être fait une erreur dans l'énoncé :
A la partie B.1°) Je met : "Soit f un élément de", ne serait-ce pas plutôt "Soit t un élément de" ?
En reprenant cet exo, je viens de remarquer que j'ai peut-être fait une erreur dans l'énoncé :
A la partie B.1°) Je met : "Soit f un élément de", ne serait-ce pas plutôt "Soit t un élément de" ?
par Zweig » 22 Juin 2010, 14:31
Salut,
Je posterai dans la soirée la généralisation de cet exercice (en remplaçant la puissance carrée par une puissance paire quelconque). SI on veut faire ça rigoureusement, il va falloir démontrer pas mal de lemmes avant (dont quelques propriétés des nombres de Bernoulli), donc ça va prendre un peu de temps pour rédiger ça (niveau T°S). Mais la démo en elle-même est beaucoup plus courte (si on prend comme vrai les propriétés des nombres de Bernoulli).
Je posterai dans la soirée la généralisation de cet exercice (en remplaçant la puissance carrée par une puissance paire quelconque). SI on veut faire ça rigoureusement, il va falloir démontrer pas mal de lemmes avant (dont quelques propriétés des nombres de Bernoulli), donc ça va prendre un peu de temps pour rédiger ça (niveau T°S). Mais la démo en elle-même est beaucoup plus courte (si on prend comme vrai les propriétés des nombres de Bernoulli).
par benekire2 » 22 Juin 2010, 15:37
si c'est abordable ... why not ? Mais je crain que ce ne soit pas le cas ...
par Dinozzo13 » 22 Juin 2010, 17:47
Il est vrai qu'une généralisation peut-être intéressante surtout pour ce type d'exercice :++:
Merci d'avance Zweig
Sinon, à propos de ma proposition, est-elle exacte ?
Merci d'avance Zweig
Dinozzo13 a écrit:B.1°) Je met : "Soit f un élément de", ne serait-ce pas plutôt "Soit t un élément de" ?
Sinon, à propos de ma proposition, est-elle exacte ?
33 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :