Term S : exponentielle, complexes

par **haricot29** » 29 Oct 2006, 19:07

Coucou tout le monde...
Eh oui on est en vacances ayé, mais malgré cela y a du boulot pour la rentrée, comme des exos de maths par exemple Grrrr
Donc voila un exo de math sur lequel j'aimerais avoir un petit coup de main SVP ! Merci d'avance, voila le sujet

Exercice :

Placer dans le plan complexe rapporté a un repère orthonormal direct (O, U(vecteur), V(vecteur)) les points A(3), B(6) et C(8+i).
On pose :
(U(vecteur) ; OC(vecteur)) = alpha [2pi]
(U(vecteur) ; AC(vecteur)) = béta [2pi]
(U(vecteur) ; BC(vecteur)) = gamma [2pi]

Montrer que alpha + béta + gamma = pi/4 [2pi]

par **Quidam** » 29 Oct 2006, 20:02

Connais-tu la formule de tangente d'une somme de deux réels ?

?

Si oui, tu n'as qu'à utiliser la formule pour calculer tan(a+b+c) !
Si non, ben, euh, faudra la démontrer, cette première formule : pas dur !

Une fois que tu auras cette formule, tu pourras calculer

à partir des tangentes de ces trois angles : tu trouveras 1, qui est

d'où tu déduiras que :

Restera à montrer que

ne peut être égal à

pour conclure que

Si ça t'ennuie, tu peux aussi calculer

et

. L'égalité des deux valeurs à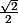

montrera que

par **rene38** » 29 Oct 2006, 20:16

Bonsoir

Autre approche :

Exprime de même

et

comme arguments de 2 nombres complexes
puis utilise Arg(z)+Arg(z')=Arg(zz')
Restera à vérifier qu'on obtient Arg(x+ix) avec x réel strictement positif.

par **fred** » 29 Oct 2006, 20:20

haricot29 a écrit:Coucou tout le monde...
Eh oui on est en vacances ayé, mais malgré cela y a du boulot pour la rentrée, comme des exos de maths par exemple Grrrr
Donc voila un exo de math sur lequel j'aimerais avoir un petit coup de main SVP ! Merci d'avance, voila le sujet

Exercice :

Placer dans le plan complexe rapporté a un repère orthonormal direct (O, U(vecteur), V(vecteur)) les points A(3), B(6) et C(8+i).
On pose :
(U(vecteur) ; OC(vecteur)) = alpha [2pi]
(U(vecteur) ; AC(vecteur)) = béta [2pi]
(U(vecteur) ; BC(vecteur)) = gamma [2pi]

Montrer que alpha + béta + gamma = pi/4 [2pi]

Tu peux commencer par calculer

et appliquer ensuite

de manière judicieuse

par **Quidam** » 29 Oct 2006, 20:27

rene38 a écrit:Autre approche...

Oui, bien sûr ! C'est évidemment plus favorable à l'entraînement sur la manipulation des complexes que ce que je suggérais !

par **haricot29** » 30 Oct 2006, 14:21

Ok merci pour tte ses infos, je vais regarder tt ça et essayer de faire mon exo avec vos infos, je mettrais mes résultats je pense en fin d'aprem ou dansl a soirée... Merci A tte !

par **haricot29** » 01 Nov 2006, 14:18

Coucou, bon je n'ai pas vu la formule avec la tangente donc je vais pencher pour la méthode de rene38 :

Autre approche :
(U(vecteur) ; OC(vecteur)) = alpha [2pi] = arg (8+i)
Exprime de même béta et gamma comme arguments de 2 nombres complexes
puis utilise Arg(z)+Arg(z')=Arg(zz')
Restera à vérifier qu'on obtient Arg(x+ix) avec x réel strictement positif.

exprimer béta et gamma :
béta = arg (5+i)
gamma = arg (2+i)
j'ai trouver ça en faisant :
(U(vecteur) ; AC(vecteur)) = béta [2pi] = (Zc-Za)/Zu(vecteur)
(U(vecteur) ; BC(vecteur)) = gamma [2pi] = (Zc-Zb)/Zu(vecteur)

C'est bon comme ça ? :hein:

par **rene38** » 01 Nov 2006, 14:31

Absolument :

donc

=...

par **haricot29** » 01 Nov 2006, 14:34

arg (8+i) + arg (5+i) + arg (2+i) = arg ((8+i)*(5+i)*(2+i)) ?!
:id:

par **rene38** » 01 Nov 2006, 14:38

Oui. Effectue le calcul.

par **haricot29** » 01 Nov 2006, 14:42

arg (8+i) + arg (5+i) + arg (2+i)
= arg ((8+i)*(5+i)*(2+i))
= arg ((40+5i+8i-1) (2+i))
= arg ((39+13i) (2+i))
= arg (78+26i+39i-13)
= arg (65+65i)
on peut écrire arg (1+i) ?

par **haricot29** » 01 Nov 2006, 14:53

:doh: c'est ok ça ?!

par **haricot29** » 01 Nov 2006, 15:01

comment fait t'on après pour montrer que arg(1+i) = pi/4 ?! :hein:

par **Quidam** » 01 Nov 2006, 15:04

haricot29 a écrit:comment fait t'on après pour montrer que arg(1+i) = pi/4 ?! :hein:

Hey ! Faut quand même lire ton cours ! Comment fait-on pour trouver l'argument de a+bi de façon générale ? C'est dans ton cours ça !

par **haricot29** » 01 Nov 2006, 15:13

oups javoue que la dessus je suis pas futte futte...c'est en effet dans mon cours en rouge ne plus
ben si on a quelque chose du type : a+bi
on peut ecrire cos téta = a/module et sin téta = b/module
donc :
cos téta = 1/rac(2) et sin 1/rac(2) --> téta = pi/4 !
ok c'est bon meric bcp !

par **haricot29** » 01 Nov 2006, 15:15

oups javoue que la dessus je suis pas futte futte...c'est en effet dans mon cours en rouge ne plus
ben si on a quelque chose du type : a+bi
on peut ecrire cos téta = a/module et sin téta = b/module
module = rac(1²+1²) = rac(2)
donc :
cos téta = 1/rac(2) et sin 1/rac(2) --> téta = pi/4 !
ok c'est bon meric bcp !

par **Quidam** » 01 Nov 2006, 15:27

Bon ! Tu as appris quelque chose aujourd'hui !

Term S : exponentielle, complexes

Term S : exponentielle, complexes

Qui est en ligne