Bonsoir. J'ai reçu un exercice de mathématique depuis une semaine, et je dois dire que je suis toujours autant bloqué. J'ai essayé pleins de choses mais rien ne fonctionne.
J'aurais donc besoin de votre aide pour m'aider à compléter ce devoir. Merci bien.
Je vous mets l'énoncé ci-dessous.
p et
q étant deux réels données, on se propose de dégager une méthode de résolution pour les équation de la forme :
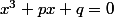
(1)
1. Lien avec les équations de degré 3 :a,
b,
c, et
d sont quatre réels, avec a différent de 0 et
 = ax^3+bx^2+cx+d)
est une fonction polynôme de degré 3. Montrer que résoudre l'équation
 = 0)
équivaut à résoudre une équation de la forme
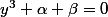
ou

et

sont deux réels à déterminer en fonction de
a,
b,
c, et
d.
Indication : on pourra poser  2. Cas triviaux pour (1) :
2. Cas triviaux pour (1) :Résoudre (1) dans le cas où
p = 0 et le cas où
q = 0.
3. Sur un exemple :On veut résoudre l'équation

(2)
a. On pose

. Que devient l'équation (2) ? Quelle valeur suffit-il de donner au produit
uv pour que l'équation (2) s'écrive

? Que vaut dans ce cas le produit
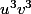
.
b. On pose
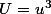
et

. Former et résoudre dans

une équation du second degré ayant pour solution U et V.
c. En déduire que :

est une solution de l'équation (2) dans

.
d. Etablir les variationde la fonction
= x^3-6x-20)
pour montrer que

est la seule solution réelle de l'équation (2).
Merci de bien vouloir m'aider.
