Bonjour, je suis un élève de 1er S. J'ai de grosse difficultés à réaliser un exercice donné en DM.
Voici l'énoncé :
Un bureau d'études est chargé de trouver une solution dont le profil sera donné par la courbe d'une fonction.
On choisit le repère orthonormé dans lequel A et B ont pour coordonnées A (0;0) et B (4;1).
La courbe doit respecter les contraintes suivantes :
Elle doit passer par les par les points A et B
Les tangentes à la courbe en ces points doivent être horizontales
1/
a) Soit f une fonction définie et dérivable sur [0;4]. On note f' sa dérivée.
Traduire les contraintes que doit respecter la courbe de f à l'aide de f et f'
J'ai répondu déjà répondu à cette question qui me donne 4 équations. Les deux premières car A et B doivent vérifier l'équation de f(x) cela donne donc f(0)=0 et f(4)=1. De plus pour prouver que les tangentes sont donc horizontales et donc parallèles à l'axe des abscisses cela donne deux équation : f'(0)=0 et f'(4)=1
b) Déterminer les réels a,b,c et d tels que la courbe de f définie par :
f(x)=ax^3+bx^2+cx+d
En utilisant la première équation, j'ai trouvé que d=0 car a*0^3+b*0^2+c*0+d=0 est équivalent à d=0
Mais je suis bloqué car je ne sais pas comment trouvé les valeurs de a,b et c
Je vous remercie d'avance pour les réponses qui pourront m'aider
Corialement Cptn Poulet
Tangente à une courbe
5 messages
- Page 1 sur 1
Re: Tangente à une courbe
Bonjour,
le début des réponses est juste.
Il n'y a que f'(4) qui est fausse. La tangente est horizontale, donc ....
Tu peux aussi calculer f(4) en fonction de a, b et c.
Ensuite, sachant que f(x)=ax^3+bx²+cx (puisque d=o comme tu l'as démontré), tu peux calculer f'(x) en fonction de a,b et c, puis tu peux y appliquer les contraintes en f' que tu connais.
Tu obtiendras ainsi de nouvelles équations en a, b et c.
le début des réponses est juste.
Il n'y a que f'(4) qui est fausse. La tangente est horizontale, donc ....
Tu peux aussi calculer f(4) en fonction de a, b et c.
Ensuite, sachant que f(x)=ax^3+bx²+cx (puisque d=o comme tu l'as démontré), tu peux calculer f'(x) en fonction de a,b et c, puis tu peux y appliquer les contraintes en f' que tu connais.
Tu obtiendras ainsi de nouvelles équations en a, b et c.
Re: Tangente à une courbe
annick a écrit:Bonjour,
le début des réponses est juste.
Il n'y a que f'(4) qui est fausse. La tangente est horizontale, donc ....
Tu peux aussi calculer f(4) en fonction de a, b et c.
Ensuite, sachant que f(x)=ax^3+bx²+cx (puisque d=o comme tu l'as démontré), tu peux calculer f'(x) en fonction de a,b et c, puis tu peux y appliquer les contraintes en f' que tu connais.
Tu obtiendras ainsi de nouvelles équations en a, b et c.
Désolé, je me suis trompé je voulais mettre f'(4)=0 mais je n'ai toujours pas compris comme faire car comme dis je cherches la valeur de a, b et c et je ne comprends pas pourquoi il faut chercher de nouvelle équation.
Re: Tangente à une courbe
4 équations aux 4 inconnues a, b, c, d :
f(0 ) =0
f(4) = 1
f'(0)=0
f'(4) = 0
Qu'est-ce qu'il te faut de plus pour résoudre ce système ?
f(0 ) =0
f(4) = 1
f'(0)=0
f'(4) = 0
Qu'est-ce qu'il te faut de plus pour résoudre ce système ?
Re: Tangente à une courbe
Bonjour
Tu as f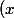=ax^3+bx^2+cx+d) et 4 équations à écrire comme dit ci-dessus. Cela c'est le truc basique.
et 4 équations à écrire comme dit ci-dessus. Cela c'est le truc basique.
Tu dois savoir écrire les 4 équations et résoudre le système.
Maintenant quand je vois ce genre de problème on peut voir sans calcul que
=x^2(w(x-4)+1)/16.) (en effet le facteur
(en effet le facteur  implique f(0)=f'(0)=0 et l'écriture du second facteur réalise l'équation f(4)=1). Il reste alors à calculer w pour vérifier la quatrième condition f'(4)=0.
implique f(0)=f'(0)=0 et l'écriture du second facteur réalise l'équation f(4)=1). Il reste alors à calculer w pour vérifier la quatrième condition f'(4)=0.
Du point de vue calcul on n'a qu'une équation au lieu de 4.
Tu as f
Tu dois savoir écrire les 4 équations et résoudre le système.
Maintenant quand je vois ce genre de problème on peut voir sans calcul que
Du point de vue calcul on n'a qu'une équation au lieu de 4.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
