Tangente et fonction exponentielle

[Maxime-59]

Bonjour,

Je viens ici pour demander de l'aide sur un exercice ou il est demandé de trouver si il existe une ou plusieurs tangentes à la courbe représentative de la fonction f qui est : parallèle(s) à la droite d'équation

On sait que deux droites son parallèles si et seulement si elles ont le même coefficient directeur. Le coefficient directeur de d d'équation y=1/4x est a.
Le coefficient directeur de Cf en a est f'(a). Une tangente à Cf est parallèle à d si et seulement si f'(a)=

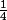
J'ai donc calculé la dérivée de la et j'ai obtenu :

Par contre, là je bloque, quelqu'un pourrait m'aider pour avancer ? Merci

[sylvainp]

Salut,
La dérivée que tu donnes n'est pas bonne, mais tu es sûr de ta fonction f?
Le raisonnement est bon sinon.

[Maxime-59]

J'avoue avoir calculé la dérivée via le site Wolframalpha car les exponentielles et les fractions dans la même dérivée ça m'a bien embrouillé !
Oui oui je suis sur de ma fonction, pourquoi ?

[sylvainp]

Ok!
non rien pour la fonction, je trouvais juste l'exercice pas bien passionant...
Tu as un quotient dans f qui se dérive comme : (u/v)'=(u'v-v'u)/v²

Tu fais ensuite l'étude f'(x)=1/4
Tu trouveras une équation à résoudre de type a*(exp(x))²+b*exp(x)+c=0

je ne sais pas où tu en es tu as peut-être avancé

[Maxime-59]

Oui oui je connaissais la formule de dérivation d'une telle fonction cependant quand j'ai posé tout ça sur ma feuille je me suis dis oulala ça va pas être facile j'ai donc utilisé Wolframalpha histoire d'avoir une "valeur sûre". Pas si sûre que ça visiblement




Et là je retombe au même résultat que précedement, ou est mon erreur ?

[Carpate]

Oui oui je connaissais la formule de dérivation d'une telle fonction cependant quand j'ai posé tout ça sur ma feuille je me suis dis oulala ça va pas être facile j'ai donc utilisé Wolframalpha histoire d'avoir une "valeur sûre". Pas si sûre que ça visiblement




Et là je retombe au même résultat que précedement, ou est mon erreur ?

Je trouve moi-aussi

[sylvainp]

Ok désolé c'est de ma faute j'avais pas pensé à simplifier comme tu as fait.
Très pratique ce Wolframalpha plus que math forum apparemment.

Ensuite tu résouds f'(x)=1/4, donc tu peux poser exp(x)=X, ne développe pas ramène toi à
4(x-3)²-(X+3)²=0 c'est de la forme a²-b²=0 donc (a-b)(a+b), tu trouves tes solutions X1 et X2 et tu reviens à x en faisant ln(X) (si tes solutions sont positives car ln d'un truc négatif tu peux pas).