Bonsoir tout le monde,voici un exercice que je ne sais pas comment meme commencer... :hein:
Soit la parabole C d'equation y = x^2 et le point S(2 ; -1).
Combien de tangeantes a C passent par S?
C'est tout,de l'aide s'il vous plait.
Tangeante issue d'un point. (1ere S)
8 messages
- Page 1 sur 1
Salut !
De quels outils tu disposes pour tout ce qui est tangente ?
Combattant204 a écrit:Bonsoir tout le monde,voici un exercice que je ne sais pas comment meme commencer... :hein:
Soit la parabole C d'equation y = x^2 et le point S(2 ; -1).
Combien de tangeantes a C passent par S?
C'est tout,de l'aide s'il vous plait.
De quels outils tu disposes pour tout ce qui est tangente ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Combattant204 a écrit:Merci pour la reponse rapide,
Sincerement je n'arrive pas a repondre exactement a votre question,que seront ces outils?
je veux dire, qu'est-ce que tu as vu en cours qui a un rapport avec ce genre d'exo ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:je veux dire, qu'est-ce que tu as vu en cours qui a un rapport avec ce genre d'exo ?
Bon moi jusqu'a present la seule chose que je pense qui peut etre utile est la fonction derivee de C.Telle que C':y = 2x sauf ca,je ne vois pas quoi faire..
Aussi C:y est deriviable sur R donc en 2.. (Fonction polynome)
Ah tu as vu les dérivées donc on peut se servir du résultat suivant :
 est la courbe représentative de la fonction "carré", qui est dérivable sur
est la courbe représentative de la fonction "carré", qui est dérivable sur 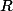 tout entier, donc quel que soit le point de
tout entier, donc quel que soit le point de  dabscisse
dabscisse  , une équation de la tangente
, une équation de la tangente  à
à  au point d'abscisse
au point d'abscisse  est :
est : 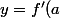(x-a)+f(a)) :+++:
:+++:
Ensuite, ça va aller très vite : d'après l'énoncé, on veut que passe par
passe par  , ou encore que
, ou encore que  , donc les coordonnées
, donc les coordonnées ) de
de  vérifient l'équation de
vérifient l'équation de  , à savoir
, à savoir (2-a)+f(a)) .
.
Donc finalement, admet au moins une tangente en un de ses points, dont on a appelé l'abscisse
admet au moins une tangente en un de ses points, dont on a appelé l'abscisse  , si et seulement si l'équation
, si et seulement si l'équation (2-a)+f(a)) admet au moins une solution :+++:
admet au moins une solution :+++:
Ensuite, ça va aller très vite : d'après l'énoncé, on veut que
Donc finalement,
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Ah tu as vu les dérivées donc on peut se servir du résultat suivant :est la courbe représentative de la fonction "carré", qui est dérivable sur
tout entier, donc quel que soit le point de
dabscisse
, une équation de la tangente
à
au point d'abscisse
est :
:+++:
Ensuite, ça va aller très vite : d'après l'énoncé, on veut quepasse par
, ou encore que
, donc les coordonnées
de
vérifient l'équation de
, à savoir
.
Donc finalement,admet au moins une tangente en un de ses points, dont on a appelé l'abscisse
, si et seulement si l'équation
admet au moins une solution :+++:
Merci! En effet j'ai tout compris et on peut meme savoir ces points (ils seront 2)
En inserons les coordonnees de S(2 ; -1) dans l'equation de T et la resoudre on aura:
T:y = 2ax - a^2
-1 = 2a2 - a^2
-1 = 4a - a^2
a^2 - 4a - 1 = 0
Delta = 20
x1 = 2 - V5 et x2 = 2 + V5
Donc les tangeantes a C aux points d'abscisses 2 - V5 et 2 + V5 passent par le point S(2 ; -1)
:lol3:
Combattant204 a écrit:Merci! En effet j'ai tout compris et on peut meme savoir ces points (ils seront 2)
En inserons les coordonnees de S(2 ; -1) dans l'equation de T et la resoudre on aura:
T:y = 2ax - a^2
-1 = 2a2 - a^2
-1 = 4a - a^2
a2 - 4a - 1 = 0
Delta = 20
x1 = 2 - V5 et x2 = 2 + V5
Donc les tangeantes a C aux points d'abscisses 2 - V5 et 2 + V5 passent par le point S(2 ; -1)
:lol3:
C'est exactement ça :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
