Tableau de Signe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Damien42530
- Membre Relatif
- Messages: 101
- Enregistré le: 23 Oct 2013, 13:11
-
 par Damien42530 » 03 Fév 2015, 14:19
par Damien42530 » 03 Fév 2015, 14:19
Bonjour , j'aimerais avoir un peu d'aide pour finir mon exercice et j'aurais d'un coup de pouce pour faire le tableau de variation / signe de g''(x) sur [0;+infini[ .
= 3 / 8(x+1)^2sqrt(x+1))
(le 3 divise tous le reste )
Merci
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 03 Fév 2015, 14:29
par Monsieur23 » 03 Fév 2015, 14:29
Aloha,
C'est g'' ou g''' que tu nous donne ?
Si c'est bien g''', alors c'est toujours positif : (x+1)^2 l'est, et Racine(x+1) aussi.
« Je ne suis pas un numéro, je suis un homme libre ! »

-
WillyCagnes
- Membre Transcendant
- Messages: 3753
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 03 Fév 2015, 14:32
par WillyCagnes » 03 Fév 2015, 14:32
bjr
sur [0;+infini[ on a
numerateur >0
denominateur tu as 8>0
(x+1)²>0
V(x+1)>0
donc g'''(x)>0
-
Damien42530
- Membre Relatif
- Messages: 101
- Enregistré le: 23 Oct 2013, 13:11
-
 par Damien42530 » 03 Fév 2015, 14:47
par Damien42530 » 03 Fév 2015, 14:47
Ok merci beaucoup , un tableau de signe serais réalisable ?
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 03 Fév 2015, 14:48
par Monsieur23 » 03 Fév 2015, 14:48
Il faudrait que tu nous donne g'' pour pouvoir en faire un tableau de signes :lol3:
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Damien42530
- Membre Relatif
- Messages: 101
- Enregistré le: 23 Oct 2013, 13:11
-
 par Damien42530 » 03 Fév 2015, 14:58
par Damien42530 » 03 Fév 2015, 14:58
Monsieur23 a écrit:Il faudrait que tu nous donne g'' pour pouvoir en faire un tableau de signes :lol3:
 = -(1/4).((sqrt(x+1))/((x+1)^2)+1/4)
Ce qui donne la dérivée :
 = (3)/8(x+1)^2sqrt(x+1))
( le 3 divise tout le reste )
Ma question est la suivante :
Déterminer alors les variations de g'' sur [0;+infini[ .
Merci
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 03 Fév 2015, 15:05
par Monsieur23 » 03 Fév 2015, 15:05
Du coup, pour les variations, g'' est croissante sur R+.
Pour le signe, calcule g''(0) : si c'est positif, alors g'' est toujours positive (puisque croissante). Sinon, il faudra trouver le moment où g''(x) = 0.
« Je ne suis pas un numéro, je suis un homme libre ! »
-
mathelot
 par mathelot » 03 Fév 2015, 15:43
par mathelot » 03 Fév 2015, 15:43
^2=(x+1)^{\frac{5}{2})
les exposants fractionnaires, c'est sympa sur R+, ici sur
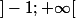
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 102 invités