Tableau de signe

[maddanlinetant]

Bonjour,

Je souhaite réaliser un tableau de signe en étudiant tout d'abord le signe de (x-1) puis (2x+3) puis le signe de (x-1) (2x+3). x doit être égal à 0 et à 3 dans ce tableau mais je sais pas quelle est la valeur interdite s'il y en a une et si le premier signe d'une ligne est égal au signe de a.
Merci

[laetidom]

Bonjour,

Je souhaite réaliser un tableau de signe en étudiant tout d'abord le signe de (x-1) puis (2x+3) puis le signe de (x-1) (2x+3). x doit être égal à 0 et à 3 dans ce tableau mais je sais pas quelle est la valeur interdite s'il y en a une et si le premier signe d'une ligne est égal au signe de a.
Merci

Bonjour,

d'après ce que je comprends, tu veux connaitre le signe de (x-1)(2x+3), c'est comme si tu voulais connaitre le signe d'une parabole (f(x)=2x²+x-3) :

déjà il n'y a pas de valeur interdite ! Par contre, il y a deux valeurs qui l'annulent (en y), ceux sont les racines.

[maddanlinetant]

Oui c'est ça je voudrais connaître leur signe !
De base, j'ai une fonction f(x) = x² + x -3 (1 + lnx)
Je l'a

[maddanlinetant]

De base j'ai une fonction f(x) = x² + x -3 (1 + lnx)
Je l'ai dérivé : (2x² + x - 3) / x
Le signe de f'(x) doit normalement être égal à (x-1) (2x+3)
Avec ses infos, je dois construire le tableau de variation de f(x) sur l'intervalle ]0 ; 3]

[laetidom]

je comprends pas trop l'objet de ton message, excuse-moi :

(x-1) <=0 pour tout x élément de ]-oo ; 1]
(x-1) >=0 pour tout x élément de ]1 ; +oo]

(2x+3) <=0 pour tout x élément de ]-oo ; -1.5]
(2x+3) >=0 pour tout x élément de ]-1.5 ; +oo]

mais après .....

[maddanlinetant]

Ben le problème c'est que je n'arrive à faire mon tableau de variation.. Je dois construire le tableau de variation de f mais je ne sais pas du tout comment faire ..

[laetidom]

De base j'ai une fonction f(x) = x² + x -3 (1 + lnx)
Je l'ai dérivé : (2x² + x - 3) / x
Le signe de f'(x) doit normalement être égal à (x-1) (2x+3)
Avec ses infos, je dois construire le tableau de variation de f(x) sur l'intervalle ]0 ; 3]

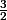
Le signe de f'(x) doit normalement être égal à (x-1) (x+) le tout sur x ??? non ?.... ah oui si x entre 0 et 3 il est positif ok

[maddanlinetant]

Le signe de f'(x) est égal à (x-1) (2x+3), je l'ai dans l'énoncé et il faut le démontrer, chose que j'ai déjà faite.
Ensuite, la question est suivante est "dresser le tableau de variation de f sur ]0 ; 3]."

[laetidom]

Le signe de f'(x) est égal à (x-1) (2x+3), je l'ai dans l'énoncé et il faut le démontrer, chose que j'ai déjà faite.
Ensuite, la question est suivante est "dresser le tableau de variation de f sur ]0 ; 3]."

(x-1) =0 pour tout x élément de ]1 ; +oo] donc >=0 pour tout x élément de [1 ; 3]

(2x+3) =0 pour tout x élément de ]-1.5 ; +oo] donc >=0 pour tout x élément de ]0 ; 3]

Donc :

(x-1)(2x+3) =0 pour tout x élément de ]1 ; 3]_______ si j'ai bien compris !!!????!!!!...

[chombier]

Bonjour,

Je souhaite réaliser un tableau de signe en étudiant tout d'abord le signe de (x-1) puis (2x+3) puis le signe de (x-1) (2x+3). x doit être égal à 0 et à 3 dans ce tableau mais je sais pas quelle est la valeur interdite s'il y en a une et si le premier signe d'une ligne est égal au signe de a.
Merci

Doublon, tu as déjà posé la même question ici : http://www.maths-forum.com/dm-fonctions-161542.php

[maddanlinetant]

C'est une question différente sur mon exercice, c'est juste pour la structure du tableau de signe car je ne sais comment le construire.

[chombier]

C'est une question différente sur mon exercice, c'est juste pour la structure du tableau de signe car je ne sais comment le construire.

Et si dans un exercice il y a 4 questions, tu vas ouvrir 4 topics ? :marteau:

[maddanlinetant]

Désolée, j'ai pas trop l'habitude des forums je n'y vais jamais..

[laetidom]

Désolée, j'ai pas trop l'habitude des forums je n'y vais jamais..

peux-tu me dire si mon message corrigé de 17h20 correspond à ton attente ou pas ? merci

[maddanlinetant]

Ma courbe décroit bien entre 0 et 1 puis croit entre 0 et 3 donc ça correspond. Mais ma question première est de savoir comment construire ce tableau de signe

[laetidom]

Ma courbe décroit bien entre 0 et 1 puis croit entre 0 et 3 donc ça correspond. Mais ma question première est de savoir comment construire ce tableau de signe

je pense que tu as voulu dire Ma courbe décroit bien entre 0 et 1 puis croit entre 1 et 3

je pensais que je t'avais mis tous les éléments pour cela à 17h20 ?, c'est bien un tableau de signes et non de variations dont tu as besoin ?....

[maddanlinetant]

Non un tableau de variations je me mélange désolée..

[laetidom]

Non un tableau de variations je me mélange désolée..

ah oui, je me disais aussi !.....

je ne vois pas ce qui te bloques ?...

tu sais que f'(x) est =0 sur [1;3]

donc que f(x) décroit sur ]0;1] et croit sur [1;3]

il te reste à trouver f(1) et les limites de f en 0+ et 3 sans oublier les racines

[maddanlinetant]

Oui ma courbe croit entre 1 et 3 désolée je mélange tout là ..

[maddanlinetant]

Désolée du coup je sais encore moins pour le coup. Comme ma courbe décroit entre 0 et 1, je fais une flèche vers le bas. Puis ma courbe croit entre 1 et 3 donc je fais une flèche vers le haut c'est bien ça ?