Systemes à trois inconnus

[taker5962]

Bonjour
Voilà j'ai un soucis
J'ai un exercice à faire, et je ne parviens pas à résoudre les deux systemes qui me sont présenter

les voici

3x - 2 y + z = -26
-2x + 3y + 2z = 22
-5x + 4y - 3z = 50

x+ y + z = 0
x + 4y + 2z = -3
3x + 2y + 4z = 1

je sais qu'il faut isoler une lettre
j'ai choisi Z dans le premier cas, et X dans le second
mais je ne parviens pas à résoudre cela

[Clembou]

Bonjour
Voilà j'ai un soucis
J'ai un exercice à faire, et je ne parviens pas à résoudre les deux systemes qui me sont présenter

les voici

3x - 2 y + z = -26
-2x + 3y + 2z = 22
-5x + 4y - 3z = 50

x+ y + z = 0
x + 4y + 2z = -3
3x + 2y + 4z = 1

je sais qu'il faut isoler une lettre
j'ai choisi Z dans le premier cas, et X dans le second
mais je ne parviens pas à résoudre cela

Excuses pour ce temps de réponse long (on ne peut pas traiter toutes les demandes, on n'est pas des robots ).

On veut résoudre :


Tu peux faire par exemple... Mais sinon, il y a une manière plus simple de résoudre des systèmes de ce genre, c'est avec le pivot de Gauss. Sais-tu ce que c'est ?

[taker5962]

non je ne sais pas du tout :hum:

[oscar]

Bonbsoir

x+y+z = 0
x+4y+2z=-3
3x+2y+4z= 1

Par substitution x = -y-z
on a
3y =z = -3
-y+2z = 1


Continue

[Clembou]

Bon ba, je vais te dire comment on fait. En fait on voudrait passer d'un système d'équations de ton type à un système d'équation de ce type :



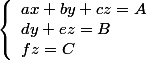
Il faut ainsi jouer sur les lignes pour obtenir ce système d'équations...

[maiscmoi]

3x-2y+z=-26 donc z=-26-3x+2y

-2x+3y+2z=22
-2x+3y+2(-26-3x+2y)=22
-2x+3y-52-6x+4y=22
-8x+7y=74

-5x+4y-3z=50
-5x+4y-3(-26-3x+2y)=50
-5x+4y+78+9x-6y=50
4x-2y=-28

tu obtiens donc deux equations
-8x+7y=74
4x-2y=-28
.......

[taker5962]

j'ai réussi à faire la seconde
par contre je ne parviens toujours pas à faire la première :hum:

[taker5962]

pour la première je suis arrivé là :
3x - 2 y + z = -26
-2x + 3y + 2z = 22
-5x + 4y - 3z = 50

z = -26 - 3x + 2y
-2x + 3y + 2(-26 - 3x + 2y) = 22
-5x + 4y - 3(-26 - 3x + 2y) = 50

z = -26 - 3x + 2y
-2x + 3y -52 - 6 x + 4y = 22
-5x + 4y +78 + 9x - 6y = 50

z = -26 - 3x + 2y
-52 - 8x + 7y = 22
+78 - 2y + 4x = 50
aprés je bloque taotalement

[maiscmoi]

tu peux simplifier

-52 - 8x + 7y = 22
+78 - 2y + 4x = 50

[Clembou]

C'est vrai que le premier système d'équation est difficile.

Transforme (2) en faisant et pour (3)

Dis moi comment est transformé ton système d'équations ?

[Timothé Lefebvre]

Yop, une question : Clément tu trouves bien des valeurs entières pour x, y et z n'est-ce pas ?

[Clembou]

Attends, je vais faire le calcul de tout ça (là je le fais plus au feeling quoi lol :lol:). Je te dis ça quand j'aurais fini :++:

[Clembou]

Après calculs, je trouve effectivement des valeurs entières de ...

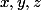
[maiscmoi]

moi en passant plus simple oui

[Timothé Lefebvre]

Ok, moi aussi : deux négatives et une positive (pour ne pas filer la réponse).

[Clembou]

Moi j'ai que des positives... :triste: J'ai du faire des erreurs de calcul lol :lol:

[maiscmoi]

moi deux positives et une negative

[Timothé Lefebvre]

Je parle bien de ce système :

3x - 2 y + z = -26
-2x + 3y + 2z = 22
-5x + 4y - 3z = 50

EDIT pour maiscmoi : combien trouves-tu ?

[taker5962]

voilà j'ai trouvé !!!
z = - 2
y = -4
x = 6

merci !!

[Timothé Lefebvre]

voilà j'ai trouvé !!!
z = - 2
y = -4
x = 6

merci !!

Voilà c'est ça !