Système - trigonométrie - valeurs absolue - paramètre

[Dinozzo13]

Bonsoir, je viens un instant de tomber sur cet exo sympa :
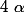
Résoudre le système de paramètre réel suivant :
; le problème est que je n'arrive pas à le faire :triste:
Voilà ce que j'ai mis pour l'instant :


[1] équivaut à .

[2] équivaut à
Après, je ne sais pas par quoi continuer.

[Ericovitchi]

De toute façon, il n'y a pas beaucoup de choix de solutions, ou bien x= alpha ou bien x = - alpha (à 2k pi près)
(il suffit de mettre alpha sur le cercle trigo et chercher les x qui marchent pour s'en convaincre)

[Ben314]

Dinozzo : tes équivalences ne vont pas : rien n'indique dans l'énoncé que cos(alpha) et sin(alpha) sont positifs (ou négatifs). Pour traduire |cos(x)|=|cos(alpha)| il semble qu'il faut faire 4 cas selon le signe de cos(x) ET de cos(alpha).
Sauf que, en fait l'équation |X|=|Y| est équivalente à [ X=Y ou bien X=-Y ] et ceci quels que soit les signes de X et Y.
Pour ta première équation, il y a donc 2 possibilités. Pour la deuxième il y a aussi deux possibilités donc, au total, il y a quatre systèmes possibles.
En fait chaque système conduit à une solution (modulo 2.pi) donc il y en en fait 4 solutions : les deux données par Ericovitchi et... deux autres que je te laisse chercher.

[Dinozzo13]

Oui, c'est bien ce que j'ai noté, non ?

[Ericovitchi]

ha oui tu as raison Ben, il y a 2 autres solutions. Comme quoi quand on va trop vite on peut passer à coté !

[Dinozzo13]

Et donc, comment dois-je poursuivre ?