Système d'inconnues
21 messages
- Page 1 sur 2 - 1, 2
Système d'inconnues
Bonsoir, je m'excuse par avance de vous déranger pour une question qui va sembler je pense très simple :
Je bloque sur une question d'un devoir, voici la dite question :
La courbe Cf passe par les points A(2,8) et B(9,1) et en S d'abscisse 5, la tangente à Cf est horizontale. En déduire alors un système d'inconnues a,b,c et, puis la résoudre. Pour finir donner l'expression de f(x).
Je ne sais vraiment pas comment m'y prendre, je sollicite donc votre aide précieuse pour m'aider dans cette question et vous en remercie.
Je bloque sur une question d'un devoir, voici la dite question :
La courbe Cf passe par les points A(2,8) et B(9,1) et en S d'abscisse 5, la tangente à Cf est horizontale. En déduire alors un système d'inconnues a,b,c et, puis la résoudre. Pour finir donner l'expression de f(x).
Je ne sais vraiment pas comment m'y prendre, je sollicite donc votre aide précieuse pour m'aider dans cette question et vous en remercie.
Re: Système d'inconnues
bjr
Il y a quelque chose qui manque dans l'énoncé.
Mais on doit deviner que la courbe est une parabole.
dc f(x)=a x ^2 +b c +c
Donc tu écris f(2)=8 et f(9)=1. ça te fait 2 équation.
La tangente horizontale correspond au somme de la parabole qui est x=-b/(2a).
Donc 5=-b/(2a).
Reste à résoudre.
Il y a quelque chose qui manque dans l'énoncé.
Mais on doit deviner que la courbe est une parabole.
dc f(x)=a x ^2 +b c +c
Donc tu écris f(2)=8 et f(9)=1. ça te fait 2 équation.
La tangente horizontale correspond au somme de la parabole qui est x=-b/(2a).
Donc 5=-b/(2a).
Reste à résoudre.
Re: Système d'inconnues
bonsoir,
on suppose que f est de la forme:
=ax^2+bx+c)
un point M de coordonnées (x;y) appartient à la courbe représentative de f si et seulement si y=f(x)
dans la formule
=ax^2+bx+c)
on a le droit de remplacer x par des valeurs.
on suppose que f est de la forme:
un point M de coordonnées (x;y) appartient à la courbe représentative de f si et seulement si y=f(x)
dans la formule
on a le droit de remplacer x par des valeurs.
Re: Système d'inconnues
Bonsoir, merci de vos réponses, est ce que ceci serait donc juste ? :
A : 8 = 4a+2b+c
B : 1 = 81a + 9b +c
S : 0 = 25a + 5b + c
Et si c'est juste, que dois-je faire après ça ?
A : 8 = 4a+2b+c
B : 1 = 81a + 9b +c
S : 0 = 25a + 5b + c
Et si c'est juste, que dois-je faire après ça ?
Re: Système d'inconnues
Salut
Tes 2 premières équations sont justes mais pas la dernière.
Tu dois exprimer le fait qu'en S d'abscisse 5, la tangente à Cf est horizontale, c'est-à-dire que le coefficient directeur de la tangente à Cf au point d'abscisse 5 est égal à 0.
Tes 2 premières équations sont justes mais pas la dernière.
Tu dois exprimer le fait qu'en S d'abscisse 5, la tangente à Cf est horizontale, c'est-à-dire que le coefficient directeur de la tangente à Cf au point d'abscisse 5 est égal à 0.
Re: Système d'inconnues
Bonjour,
Pour exprimer ce coefficient directeur qui égale à 0, je dois utiliser -b/2a ? et si oui que faire avec ça, je ne sais vraiment pas.
Pour exprimer ce coefficient directeur qui égale à 0, je dois utiliser -b/2a ? et si oui que faire avec ça, je ne sais vraiment pas.
Re: Système d'inconnues
Si tu as vu les dérivées, tu dois pouvoir exprimer le coefficient directeur de la tangente à Cf au point d'abscisse 5 en fonction de a et b.
Sinon tu utilises les propriétés des paraboles. La tangente est horizontale au sommet de la parabole, qui a pour abscisse -b/(2a).
Sinon tu utilises les propriétés des paraboles. La tangente est horizontale au sommet de la parabole, qui a pour abscisse -b/(2a).
Re: Système d'inconnues
Bonsoir,
Je suis désolé mais je ne vois comment faire avec ces informations....
Je suis désolé mais je ne vois comment faire avec ces informations....
Re: Système d'inconnues
Bonsoir,
As-tu étudié les paraboles en cours ?
Si oui as-tu appris qu'une parabole de la forme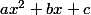 passe par un sommet au point d’abscisse
passe par un sommet au point d’abscisse  ?
?
As-tu étudié les paraboles en cours ?
Si oui as-tu appris qu'une parabole de la forme
Re: Système d'inconnues
Bonsoir,
Oui ça je le sais; ce que je ne sais pas c'est que dois-je faire de cette information ?
Oui ça je le sais; ce que je ne sais pas c'est que dois-je faire de cette information ?
Re: Système d'inconnues
Dans l'énoncé on indique "en S d'abscisse 5, la tangente à Cf est horizontale", tu peux déduire que ce point d’abscisse 5 correspond à 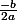
Ce qui va te donner une nouvelle équation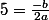
Ce qui va te donner une nouvelle équation
Re: Système d'inconnues
Tu avais déjà 2 équations, avec cette 3ème tu vas pouvoir trouver les valeurs de a, b et c ...
Re: Système d'inconnues
Tu pouvais également partir de "en S d'abscisse 5, la tangente à Cf est horizontale" ce qui correspond à la dérivée en ce point est égale à 0
f'(x)=2ax+b en remplaçant x par 5 tu obtiens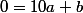 ce qui est équivalent à ce que tu trouves en partant de la propriété que la parabole passe par un sommet au point d'abscisse
ce qui est équivalent à ce que tu trouves en partant de la propriété que la parabole passe par un sommet au point d'abscisse 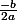
... c'est plutôt rassurant on retrouve la même équation que précedemment
f'(x)=2ax+b en remplaçant x par 5 tu obtiens
... c'est plutôt rassurant on retrouve la même équation que précedemment
Re: Système d'inconnues
Merci de votre réponse, je bloque maintenant sur la résolution du système, je ne sais pas quelle méthode utiliser 

Re: Système d'inconnues
C'est bon j'ai réussi, merci encore de votre aide, j'ai maintenant une autre question à poser (je ne sais pas si je dois faire un autre post), je dois calculer la limite de [f(x)-(x-10)] x -> + infini et euh comment dire que les limites c'est encore pire, je ne sais pas du tout m'y prendre 

Re: Système d'inconnues
C'est bon pour les valeurs de a,b et c 
Comment procèdes-tu habituellement pour calculer une limite ?
Comment procèdes-tu habituellement pour calculer une limite ?
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
