Système de 3 équations et 3 inconnus

par **Ross** » 29 Aoû 2006, 16:51

Bonjours !!

Alors aujourd'hui, je vous présente mon premier système de 3 équations à 3 inconnus :

3x+2y-5z=8
x- y + z=2
4x-5y+3z=5

Donc comme s'habitude, essayant 3 fois jusqu'au bout ce système, j'en est eu marre donc si vous pouviez me donner un indice s'il vous plaît ? Je vous en serez très reconnaissant ( comme toujours :) ). Merci !

par **fonfon** » 29 Aoû 2006, 16:53

Salut,

3x+2y-5z=8
x- y + z=2
4x-5y+3z=5

quelle méthode as-tu utilisé pour résoudre ce système?

par **nekros** » 29 Aoû 2006, 17:02

Salut,

Je note L1 la première ligne, L2 la seconde et L3 (devine...)

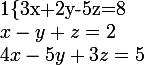
En faisant 5L2+L1 et 5L3+3L1, le système devient :

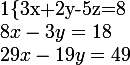
On s'est débarassé du z.

En combinant les deux dernières lignes, tu isoles x.
Ensuite, tu "remontes" le système pour trouver y (en remplaçant x dans la seconde équation)
Enfin, tu trouves z grâce à la première équation.

A+

par **fonfon** » 29 Aoû 2006, 17:04

Re, on doit trouver

sauf erreur

par **nekros** » 29 Aoû 2006, 17:10

fonfon a écrit:sauf erreur

Il n'y en a pas. :happy3:

A+

par **huntersoul** » 29 Aoû 2006, 17:19

[quote="Ross"]Bonjours !!

3x+2y-5z=8
x- y + z=2
4x-5y+3z=5
si on aditionne tous on aura
8x-4y-z=15
et -z=x-y-2
donc 8x-4y+x-y=17
et4x-5y+3z=5
donc 4x-5y+3(2-x+y)
4x-5y+6-3x+3y=5
x-2y=-1
alors9(2y-1)-5y=17
13y=26
y=2
et puisque x=2y-1=4-1=3
et 3-2+z=2 donc z=1
c'est un peu endésordre mé bon
à+

par **fonfon** » 30 Aoû 2006, 08:24

Salut, moi je l'ai fait par substitution:

donc S=...
A+

par **Ross** » 30 Aoû 2006, 08:32

Merci les gars pour votre aide. Je pense que n'ayant jamais fait de système à trois inconnus jusqu'à présent, je vais me contenter de la méthode par substitution :lol4: Mais j'ai bien pris soin de comprendre les autres méthodes.
Allez, à la prochaine fois !

par **fonfon** » 30 Aoû 2006, 08:34

DE rien et à la prochaine fois :happy2:

Système de 3 équations et 3 inconnus

Système de 3 équations et 3 inconnus

Qui est en ligne