Système d'équation d'un droite orthogonale à un plan

[etrangedromadaire]

Bonjour, je suis bloqué à la 3 ème question (et je ne peux pas faire les autres questions sans la réponse à celle ci) de cet exercice d'entrainement pour un futur DS.
Pouvez vous m'aider ?

Sujet :

On considère un cube ABCDEFGH. Le point M est le milieu de [BF], I le milieu de [BC], le point est est défini par la relation CN=1/2GC et le point P est le centre de la face ADHE.
1. Justifier que la droite (MN) coupe le segment [BC] en son milieu I. 
On munit l'espace du repère orthonormé (A; AB;AD;AE). 
2. Justifier que le vecteur n (1 2 2) est un vecteur normal au plan (MNP). En déduire une équation cartésienne du plan (MNP). 
3. Déterminer un système d'équations paramétriques de la droite (d) passant par G et orthogonale au plan (MNP). 
4. Montrer que la droite (d) coupe le plan (MNP) au point K de coordonnées (2/3;1/3;1/3) En déduire la distance GK. 

2. équation cartésienne du plan (MNP) x+2y+2z-2=0
3. n est un vecteur normal à (MNP) et est donc un vecteur directeur de (d) qui est orthogonale à ce plan en passant par G donc je pensais faire cela :
G(1;1;1)
x=1+k
y=1+2k
z=1+2k k€IR
Mais c'est faux puisqu'à la question suivante je ne trouve pas la bonne réponse...
Pouvez vous m'indiquer la méthode à utiliser pour la question 3 ? Merci !

[Carpate]

La droite (d) est la droite passant par G et parallèle à 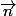(1; 2 ; 2)
Tout point M (x,y, z) de (d) vérifie donc la relation : avec k réel ce qui se traduit par le système de 3 équations paramétriques :frac13



On a l'habitude d'utiliser plutôt le réel t comme paramètre..
Ta réponse est correcte. que trouves-tu à la question 3 ?

EDIT
Les coordonnées du point K vérifie le système paramétrique et l'équation du plan (MNP)donc :
ce qui donne



Tout baigne !

J'ai un pb d'éditeur qui m'insère des morceaux de texte quand je déplace la souris !!

[hdci]

Bonjour,
Je trouve bien le même système... Et je trouve bien les bonnes coordonnées du point d'intersection.

Comment avez-vous fait ?