Système avec paramètre

par **Dante0** » 23 Sep 2012, 08:44

chan79 a écrit:ce triplet (x,y,z) que tu as trouvé est donc la solution (point d'intersection des 3 plans) sauf dans le cas où a=-3 (les dénominateurs seraient nuls).
Que peut-on dire sans le cas où a=-3 ?

Je suppose que c'est ce que tu as dis la dernière fois : "donc l'intersection des trois plans est soit un point, soit l'ensemble vide."
En fait uniquement 2 plans se croisent c'est cela ? Tu dis que : "On remarque que A n'est pas un point du plan défini par la troisième égalité ( quel que soit a)" mais à quoi tu le vois ?

par **chan79** » 23 Sep 2012, 08:51

Dante0 a écrit:Je suppose que c'est ce que tu as dis la dernière fois : "donc l'intersection des trois plans est soit un point, soit l'ensemble vide."
En fait uniquement 2 plans se croisent c'est cela ? Tu dis que : "On remarque que A n'est pas un point du plan défini par la troisième égalité ( quel que soit a)" mais à quoi tu le vois ?

remplace x par -4, y par -5 et z par 0 dans la troisième égalité

par **Dante0** » 23 Sep 2012, 08:57

chan79 a écrit:remplace x par -4, y par -5 et z par 0 dans la troisième égalité

J'obtiens 7 = 2 ok.
D'ailleurs je voulais revenir sur l'une de tes phrases au début que j'avais pas compris tu dis : "On peut déjà remarquer que l'intersection des plans définis par les deux premières équations est la droite qui passe par A(-4,-5,0) et dirigée par le vecteur (2,3,1). (il suffit de résoudre avec z comme paramètre)."

Comment vois-tu qu'elle passe par ce point A et que veux dire le fait qu'elle soit dirigée par le vecteurs de telles coordonnées ? J'ai vu les places qu'occupent ces valeurs dans les equations mais ca se passe comment en fait ? C'est comme le coefficient directeur et l'ordonnée à l'origine avec les fonctions affines ?

par **chan79** » 23 Sep 2012, 09:05

Dante0 a écrit:J'obtiens 7 = 2 ok.
D'ailleurs je voulais revenir sur l'une de tes phrases au début que j'avais pas compris tu dis : "On peut déjà remarquer que l'intersection des plans définis par les deux premières équations est la droite qui passe par A(-4,-5,0) et dirigée par le vecteur (2,3,1). (il suffit de résoudre avec z comme paramètre)."

Comment vois-tu qu'elle passe par ce point A et que veux dire le fait qu'elle soit dirigée par le vecteurs de telles coordonnées ? J'ai vu les places qu'occupent ces valeurs dans les equations mais ca se passe comment en fait ? C'est comme le coefficient directeur et l'ordonnée à l'origine avec les fonctions affines ?

x=-4+2z
y=-5+3z
si z=0 tu as (-4,-5,0)

par **Dante0** » 23 Sep 2012, 09:11

chan79 a écrit:x=-4+2z
y=-5+3z
si z=0 tu as (-4,-5,0)

Oui j'ai compris ca.
Mais pourquoi l'intersection c'est A(-4,-5,0) et pas (2,3,1) ? Il y'a une règle non ? :mur:

par **chan79** » 23 Sep 2012, 09:15

Dante0 a écrit:Oui j'ai compris ca.
Mais pourquoi l'intersection c'est A(-4,-5,0) et pas (2,3,1) ? Il y'a une règle non ? :mur:

l'intersection des deux premiers plans est une droite qui pzasse entres autres par (-4,-5,0) et qui est dirigée par le vecteur (2,3,1)

par **Dante0** » 23 Sep 2012, 09:23

chan79 a écrit:l'intersection des deux premiers plans est une droite qui pzasse entres autres par (-4,-5,0) et qui est dirigée par le vecteur (2,3,1)

Oui mais je veux comprendre pourquoi ? Il y'a une propriété ?
Pourquoi on ne dis pas que l'intersection des deux premiers plans est une droite qui passe entres autres par (2,3,1) et qui est dirigée par le vecteur (-4,-5,0) ??
Autrement dit quand tu observes l'equation à quoi reconnais-tu les coordonnées de l'intersection et les coordonnées du vecteurs ?

par **chan79** » 23 Sep 2012, 09:38

Dante0 a écrit:Oui mais je veux comprendre pourquoi ? Il y'a une propriété ?
Pourquoi on ne dis pas que l'intersection des deux premiers plans est une droite qui passe entres autres par (2,3,1) et qui est dirigée par le vecteur (-4,-5,0) ??
Autrement dit quand tu observes l'equation à quoi reconnais-tu les coordonnées de l'intersection et les coordonnées du vecteurs ?

tu as vu les systèmes d'équations paramétriques des droites ?

par **Dante0** » 23 Sep 2012, 09:40

chan79 a écrit:tu as vu les systèmes d'équations paramétriques des droites ?

Non ou du moins ca remonte à pas mal de temps...
Mais il faut que je sache, je suis sur que c'est pas compliqué.

par **chan79** » 23 Sep 2012, 09:47

Dante0 a écrit:Non ou du moins ca remonte à pas mal de temps...
Mais il faut que je sache, je suis sur que c'est pas compliqué.

Bon, à partir des deux premières équations , tu as
x=-4+2z
y=-5+3z
z= 0+1z qui est toujours vrai que je rajoute
Soit M(x,y,z)
Soit A(-4,-5,0)

(2,3,1)
M appartient à l'intersection des deux plans si
x+4=2z
y+5=3z
y=1y
Autrement dit si les vecteurs

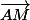
et

sont colinéraires
L'interscetion des 2 demi-plans est une droite qui est définie par le point A et le vecteur

.

par **chan79** » 23 Sep 2012, 09:51

Sur ce dessin, on voit en noir la droite qui est l'intersection des deux premiers plans (vert et bleu)
En rouge le troisième plan dans le cas a=-3, il ne coupe pas cette droite
[img][IMG]http://imageshack.us/a/img228/3756/17683495.png[/img][/IMG]

par **Dante0** » 23 Sep 2012, 09:53

Bon ok

DOnc quand on me demande résoudre selon les valeur de a la réponse c'est :

pour tout a différent de -3 ?

Je peux aussi ajouter qu'en règle générale l'intersection de 3 plans est un point ?

par **chan79** » 23 Sep 2012, 10:02

Dante0 a écrit:Bon ok
DOnc quand on me demande résoudre selon les valeur de a la réponse c'est :

pour tout a différent de -3 ?

Je peux aussi ajouter qu'en règle générale l'intersection de 3 plans est un point ?

oui, si a est différent de -3 tu as le point que tu as écrit
si a=-3 pas de point d'intersection (dessin précédent)
Ci-dessous pour a=2 tu as le point d'intersection (-0,4;0,4;1,8) (gros point rouge)
[img][IMG]http://imageshack.us/a/img69/8392/93168895.png[/img][/IMG]

par **chan79** » 23 Sep 2012, 10:06

chan79 a écrit:oui, si a est différent de -3 tu as le point que tu as écrit
si a=-3 pas de point d'intersection (dessin précédent)
Ci-dessous pour a=2 tu as le point d'intersection (-0,4;0,4;1,8) (gros point rouge)
[img][IMG]http://imageshack.us/a/img69/8392/93168895.png[/img][/IMG]

En général, l'intersection de trois plans est un point (si tu tapes au hasard trois équations de plans, il y a de grandes chances pour que ce soit le cas) mais ça peut être aussi l'ensemble vide, une droite ou même un plan, si les trois plans sont confondus).
Dans ton exo, c'est soit un point, soit l'ensemble vide.

par **Dante0** » 23 Sep 2012, 10:13

Merci pour ta patience ! :)
J'ai un dernier système à 4 inconnues à résoudre, j'essaye de le faire seul.

par **chan79** » 23 Sep 2012, 10:16

Dante0 a écrit:Merci pour ta patience !

Pas de souci, content de t'aider

par **Dante0** » 23 Sep 2012, 10:51

Voici l'énoncé :

Résoudre par la méthode du pivot et avec représentation matricielle, le système suivant selon les valeurs du paramètre b.

J'ai d'abord trouvé

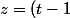Ensuite

Donc

Ca me parait archi faux... :hum:

par **Dlzlogic** » 23 Sep 2012, 11:01

Bonjour,
Dans l'énoncé, il n'est pas dit qu'il fait le résoudre par la méthode du pivot avec présentation matricielle ?

par **Dante0** » 23 Sep 2012, 11:17

Dlzlogic a écrit:Bonjour,
Dans l'énoncé, il n'est pas dit qu'il fait le résoudre par la méthode du pivot avec présentation matricielle ?

Oui c'est ce que j'ai fait mais je suis censé faire quoi du paramètre b ? J'ai pensé que ca se rapprochait de l'exercice précédent...
Pour la représentation matricielle, je comment représenter le système avec une matrice mais je ne sais pas comment détailler les étapes de calculs avec les matrices.

par **Dante0** » 23 Sep 2012, 13:21

J'ai repris le système et appliqué la méthode du pivot pour voir ou ca allait me mener, et je trouve b = 0 ? C'est normal que je trouve directement la valeur de b ? Je suis censé résoudre selon les valeurs de b non ?

Système avec paramètre

Qui est en ligne