Bonjour a tous,
Je bloque sur un nouveau problème:
f est une fonction définie sur R telle que, pour tout réel de x: f(x)+f(-x)=2
On note C sa courbe représentative dans un repère orthogonal du plan. Alors C est symétrique par rapport:
a) à la droite d'équation x=1
b) à la droite d'équation x=2
c) à l'origine du repère
d) au point de coordonnées (0,1)
e) au point de coordonnées (0,2)
Merci d'avance
Symétrie courbe représentative
3 messages
- Page 1 sur 1
Re: Symétrie courbe représentative
Bonjour
la réponse c'est D). Pour le voir il suffit de translater ton graphe vers le bas d'une unité.
Plus précisément tu poses g(x)=f(x)-1 et tu vois que g est impaire.
la réponse c'est D). Pour le voir il suffit de translater ton graphe vers le bas d'une unité.
Plus précisément tu poses g(x)=f(x)-1 et tu vois que g est impaire.
Re: Symétrie courbe représentative
Bonjour;
Un exemple d'une telle fonction est la fonction polynomiale définie sur
définie sur  par :
par :
 =1+\Sum_{k=0}^n a_kx^{2k+1}) avec
avec \in\mathbb N^2) et les
et les  .
.
On a :=1+a_0x) et
et 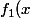=1+a_0x+a_1x^3) .
.
Soit aussi la fonction définie et impaire sur
définie et impaire sur  ; donc la fonction
; donc la fonction  définie sur
définie sur  par :
par :
 = 1+g(x)) , est aussi un exemple d'une telle fonction .
, est aussi un exemple d'une telle fonction .
On a : + f(- x) = 1 + g(x) + 1 + g(- x) = 2 + g(x) - g(x) = 2) .
.
Un exemple d'une telle fonction est la fonction polynomiale
On a :
Soit aussi la fonction
On a :
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
