Dm sur suites

par **marseille123** » 23 Fév 2008, 12:15

[FONT=Comic Sans MS]bjr tout le monde j'ai un problème avec un dm de math que je n'arrive pas à résoudre..alors je me suis dis que je pouvais trouver de l'aide sur ce forum .. voici mon énoncé :

soit (Un) la suite définie par :

> Un =

((2)+;)((2)+;)((2)+;)+;)(2))))

( avec n fois le nombre 2 sous les radicaux )
> ma question est démontrer que la suite (Un) est convergente .

la suite Un on le voit pas trop parce que c'est mal représenté mais à chaque fois que l'on rajoute +racine2 , elle vient se rajouter dans la racine précédente et ainsi dessuite . je n'arrive pas à placer le nombre "n" à l'intérieur et je ne peux pas non plus trouver Un+1 ni les autres résultat.. j'ai trouver avec ma calculatrice en faisant à chaque fois un ajout de racine2 que la suite tendait vers 2 quand elle grandit . et j'en suis ici ...
J'accepterais la moindre aide avec grand plaisir car je ne sais plus quoi faire .. en vous remerciant d'avance

man
[/FONT]

par **elguardito** » 23 Fév 2008, 13:38

Bah pour prouver qu'elle converge, faut montrer qu'elle a une limite finie en +infini.
Donc si je comprends bien l'énoncé u(n) peut s'écrire comme:
u(n)=(V2)^n
C'est sa?
V=racine carré

par **marseille123** » 23 Fév 2008, 13:46

enfet je narive pa a bien marquer lénoncé de la suite parceke les racine elle sarete avan le 2 sur ce forum alor ke la premiere racine ds mon enoncée ell continu juskau bou et dedan a chak foi on ajoute racine de 2 et a chake foi la racine el continu juska bou . et sa continu an ajouté racine de 2 toujour a linterieur de la racine precedente juska sareter a racine 2 au final. je ne sais pa comment lexpliké . jai scanné mon dm si tu veu ? jpe te lenvoyé par mail .. mai jpense ke ta reponse avec la puissance n ta du comprendre kon fesai la somme de racine de 2 c pr sa . mais deja merci mek parceke tma rep c cool..

par **elguardito** » 23 Fév 2008, 13:50

C'est normal on est là pour s'entraider ;)
Ce que tu peux faire c'est l'héberger plutot sa sera mieux genre sur Zshare ou autre comme sa tous ceux qui veulent t'aider auront le sujet.

par **marseille123** » 23 Fév 2008, 14:33

Zshare ? c koi c un forum ou jpe metre mes image et tout ?

par **marseille123** » 23 Fév 2008, 14:35

ah c bn jai compri . enfet jmet mon fichier sur internet pi jlache le lien html et c bon . merci mec. mai jsp jv men sortir jai vmt rien compri :s

vla c mon fichier http://www.zshare.net/image/8002231ecdda8b/

par **marseille123** » 24 Fév 2008, 13:52

svp les gens jsui en galere grav la :s

par **elguardito** » 24 Fév 2008, 13:58

J'ai beau cherché je ne vois pas.
A mon avis faut exprimer u(n) en intégrant un n de façon à prouver que lorsque n tent vers +infini, u(n) tend vers 2. Mais comment :hein: ??

par **marseille123** » 24 Fév 2008, 14:25

ué lol cmt ? tkt mek tan pi

par **Sa Majesté** » 24 Fév 2008, 15:17

Voilà enfin un exo à peu près intéressant où on ne te mâche pas le travail et où il faut faire preuve d'un peu d'imagination
Pose

et pour tout n

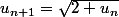
Etudie la suite

Montre qu'elle est croissante et majorée, et qu'elle converge vers 2
Et arrête d'écrire en SMS :hum:

par **marseille123** » 26 Fév 2008, 21:34

merci mec tu t'es gavé merci serieu

par **Sa Majesté** » 27 Fév 2008, 20:30

marseille123 a écrit:merci mec tu t'es gavé merci serieu

Quelqu'un peut me dire comment il faut le prendre ? :stupid_in

Dm sur suites

Dm sur suites

Qui est en ligne