[Fini] DM sur les tengentes
39 messages
- Page 1 sur 2 - 1, 2
[Fini] DM sur les tengentes
Bonjour,
J'ai à rendre dans une semaine, un DM de maths sur les tangentes avec lequel je suis en galère totale, je mélange tout, les limites etc. J'aimerais s'il vous plaît, que l'on m'explique ce qu'il faut faire afin de résoudre ce problème. Les maths étant de loin mon point fort, je suis un peu perdu.
Cordialement
J'ai à rendre dans une semaine, un DM de maths sur les tangentes avec lequel je suis en galère totale, je mélange tout, les limites etc. J'aimerais s'il vous plaît, que l'on m'explique ce qu'il faut faire afin de résoudre ce problème. Les maths étant de loin mon point fort, je suis un peu perdu.
Cordialement
- Fichiers joints
-
- Photo du DM + énoncé
- dm de maths.jpg (84.25 Kio) Vu 907 fois
Modifié en dernier par Aquatwix le 09 Jan 2017, 09:39, modifié 1 fois.
Re: DM de maths : tangentes (1STI)
Aquatwix a écrit:Bonjour,
J'ai à rendre dans une semaine, un DM de maths sur les tangentes avec lequel je suis en galère totale, je mélange tout, les limites etc. J'aimerais s'il vous plaît, que l'on m'explique ce qu'il faut faire afin de résoudre ce problème. Les maths étant de loin mon point fort, je suis un peu perdu.
Cordialement
Salut,
On se place en un point L (L pour "Laser") de la courbe, d'abscisse a (a est un nombre).
Puisque L est un point de la courbe de f, son ordonnée vaut
Le but sera de trouver le point "a" pour que la tangente à la courbe au point a passe par le point (2;3).
L'équation de la tangente au point a est donnée par:
1) Que vaut f'(a) ?
2) Comment traduire le fait que (2;3) appartient à la droite
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
Bonjour Lostounet et merci pour ta réponse,
Donc si j'ai bien compris je dois trouver par le graphique le coefficient directeur de a mais comment le dire ou le démontrer à l'écrit ?
Pour le 2) si j'en suis ton équation je suppose que je dois faire les limites ?
En totu cas merci pour ta réponse
Donc si j'ai bien compris je dois trouver par le graphique le coefficient directeur de a mais comment le dire ou le démontrer à l'écrit ?
Pour le 2) si j'en suis ton équation je suppose que je dois faire les limites ?
En totu cas merci pour ta réponse
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
Aquatwix a écrit:
Donc si j'ai bien compris je dois trouver par le graphique le coefficient directeur de a mais comment le dire ou le démontrer à l'écrit ?
On parle de coefficient directeur d'une droite (ici la droite tangente au point a) qui a pour coefficient directeur f'(a). Si tu ne comprends pas le terme de "coefficient directeur" tu peux le remplacer par "pente" ou bien "inclinaison".
On ne va pas le faire graphiquement mais par le calcul. Si
Aquatwix a écrit:Pour le 2) si j'en suis ton équation je suppose que je dois faire les limites ?
Qui a jamais parlé de limite ? Dans le sujet ou dans mon post... Les limites n'ont rien à voir avec cet exercice.
S'il te plait relis .. Je te demande quelque chose de très simple:
Si tu as une droite y =mx + p avec m = 3 par exemple, et qui passe par un point disons (1;2), comment tu fais pour trouver p ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
Pour le 1 je pense que j'ai compris.
Pour le 2, p c'est l'endroit où coupe la droite sur l'axe des ordonnés, soit 2 ?
Merci de prendre du temps pour m'expliquer
Pour le 2, p c'est l'endroit où coupe la droite sur l'axe des ordonnés, soit 2 ?
Merci de prendre du temps pour m'expliquer
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
On peut donc commencer par le 1), que vaut f'(a) ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
Dans mon tableau des dérivés, je sais que x² vaut 2x.
f(x)=x²+1 donc f'(x)=2x+1 ?
f(x)=x²+1 donc f'(x)=2x+1 ?
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
La dérivé d'une constante comme 1 vaut 0.
Donc f'(x) = 2x + 0 = 2x
Donc nous avons bien f'(a) = 2a
Donc f'(x) = 2x + 0 = 2x
Donc nous avons bien f'(a) = 2a
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
Ah oui effectivement, bon jusque là j'ai compris, je prends des notes.
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
Aquatwix a écrit:Pour le 2, p c'est l'endroit où coupe la droite sur l'axe des ordonnés, soit 2 ?
Oui, p est l'ordonnée à l'origine (cela signifie que c'est l'ordonnée du point d'intersection de la droite avec l'axe des ordonnées, et ce point on sait qu'il est d'abscisse 0!)
Par contre, ici p ne vaut pas 2 (car je ne t'ai pas dit que la droite passe par le point (0;2), donc 2 n'est pas l'ordonnée du point d'abscisse 0).
Pour te rappeler un peu: si un point appartient à une droite d'équation y = mx + p, alors ses coordonnées vérifient l'équation de cette droite. Cela signifie que si par exemple elle passe par (1;2), alors:
2 = m*1 + p (on remplace y par 2 et x par 1 pour traduire cela)
Si en plus la pente m vaut 3, alors 2 = 3*1 + p ce qui permet de trouver p (p = 2 - 3=-1).
Pour revenir à l'exercice:
Tu as une certaine droite:
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
D'accord, merci de m'avoir éclairé, je vais réfléchir un peu de mon côté, je reviens vous voir dans une petite heure afin de vous faire part de mes résultats. Merci encore 
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
Si tu as des lacunes ce n'est pas grave... courage!
S'il te faut en plus des rappels sur des bases, et que tu es motivé, nous pouvons t'aider. Essaye de comprendre les choses petit à petit (si tu ne comprends pas exactement, il faut revenir dessus...)
S'il te faut en plus des rappels sur des bases, et que tu es motivé, nous pouvons t'aider. Essaye de comprendre les choses petit à petit (si tu ne comprends pas exactement, il faut revenir dessus...)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
Et oui j'ai quelques lacunes surtout en maths, c'est la matière auquelle je m'intéresse le moins et pourtant c'est l'une des plus importante.. Je vais bien bien y bosser, je suis motivé j'espère que je m'en sortirai.
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
C'est un cercle vicieux: moins on s'y intéresse, moins on s'en sort, et plus c'est pénible... moins on s'en sort.
Comme le sport: si on en fait pas, on grossit, on en fait moins, on grossit encore ...
La solution? Casser le cycle: Essayer de comprendre. Comprendre prend bien plus de temps que de résoudre des exercices (et c'est plus difficile!), mais sur le long terme cela paye plus: donc par exemple ici, plutôt que de te concentrer uniquement sur le dm, tu peux essayer de revenir sur les choses non comprises et te poser des questions. Comme un lecteur ! C'est quoi la pente d'une droite? C'est quoi la dérivée d'une fonction concrètement...? Pourquoi l'équation de la tangente en un point de la courbe est y = .. et pas autre chose?).
J'ai suivi un étudiant qui avait 2 en maths... et une fois je l'ai poussé dans la bonne direction (comprendre plutôt que d'apprendre, et d'appliquer bêtement) et il est passé à 14. Pas "seulement" grâce à moi , mais grace à un changement de méthode et beaucoup de volonté
, mais grace à un changement de méthode et beaucoup de volonté
Courage
Comme le sport: si on en fait pas, on grossit, on en fait moins, on grossit encore ...
La solution? Casser le cycle: Essayer de comprendre. Comprendre prend bien plus de temps que de résoudre des exercices (et c'est plus difficile!), mais sur le long terme cela paye plus: donc par exemple ici, plutôt que de te concentrer uniquement sur le dm, tu peux essayer de revenir sur les choses non comprises et te poser des questions. Comme un lecteur ! C'est quoi la pente d'une droite? C'est quoi la dérivée d'une fonction concrètement...? Pourquoi l'équation de la tangente en un point de la courbe est y = .. et pas autre chose?).
J'ai suivi un étudiant qui avait 2 en maths... et une fois je l'ai poussé dans la bonne direction (comprendre plutôt que d'apprendre, et d'appliquer bêtement) et il est passé à 14. Pas "seulement" grâce à moi
 , mais grace à un changement de méthode et beaucoup de volonté
, mais grace à un changement de méthode et beaucoup de volontéCourage
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
Je prends vos conseils en compte, je vais essayé de travailler dessus, en tout cas merci de m'aider, mon prof est assez bizard, il ne nous explique les choses pas plus que ça.
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
Pour en revenir sur le DM partie 2, j'ai vérifié l'équation de droite : y=mx + p
Donc on sait que y=3 et x=2 donc : 2 = m*3 + p
Et d'après le dessin le coefficient directeur semble être 2 ( monté sur avancé )
Donc 2 = 2*3 + p
2-6 = p
-4 = p
C'est ensuite que je ne sais plus quoi faire ..
Donc on sait que y=3 et x=2 donc : 2 = m*3 + p
Et d'après le dessin le coefficient directeur semble être 2 ( monté sur avancé )
Donc 2 = 2*3 + p
2-6 = p
-4 = p
C'est ensuite que je ne sais plus quoi faire ..
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
Aquatwix a écrit:Pour en revenir sur le DM partie 2, j'ai vérifié l'équation de droite : y=mx + p
Donc on sait que y=3 et x=2 donc : 2 = m*3 + p
Et d'après le dessin le coefficient directeur semble être 2 ( monté sur avancé )
Donc 2 = 2*3 + p
2-6 = p
-4 = p
C'est ensuite que je ne sais plus quoi faire ..
Bonsoir,
si y=mx+p avec (2;3)
alors 3 = m.2 + p
De plus, si m vaut 2 alors 3 = 2.2 + p ===> p = 3 - 4 = - 1
Modifié en dernier par laetidom le 07 Jan 2017, 20:32, modifié 3 fois.
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
C'est le principe.
Mais l'équation de la droite est de la forme:
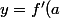 (x - a) + f(a)) qui passe par le point (2;3). Cela signifie que les coordonnées (2;3) vérifient l'équation de cette droite... donc on remplace y par 3 et x par 2. Donc:
qui passe par le point (2;3). Cela signifie que les coordonnées (2;3) vérifient l'équation de cette droite... donc on remplace y par 3 et x par 2. Donc:
(2 - a) + f(a))
Il suffit maintenant de remplacer f(a) et f'(a) par leurs valeurs en fonction de a.
On obtient une équation du 2nd degré pour trouver a.
Mais l'équation de la droite est de la forme:
Il suffit maintenant de remplacer f(a) et f'(a) par leurs valeurs en fonction de a.
On obtient une équation du 2nd degré pour trouver a.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
f(a)=a²+1 / f'(a)=2a
Donc :
y=f'(a)(x-a)+f(a)
3=2a(2-a)+a²+1
3=4a+(-2a²)+a²+1
3=4a+a²+1
2=4a+a²
Ensuite c'est bloqué ... je suis vraiment nul..
Donc :
y=f'(a)(x-a)+f(a)
3=2a(2-a)+a²+1
3=4a+(-2a²)+a²+1
3=4a+a²+1
2=4a+a²
Ensuite c'est bloqué ... je suis vraiment nul..
Re: DM de Maths (1STI) : Les Tangentes, tâche complexe.
Aquatwix a écrit:f(a)=a²+1 / f'(a)=2a
Donc :
y=f'(a)(x-a)+f(a)
3=2a(2-a)+a²+1
3=4a+(-2a²)+a²+1
3=4a+a²+1.
C'est
Qui est équivalente à
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
39 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
