Bonjour j'ai un dm sur les probabilités, il y a un exercice que je n'arrive pas à faire:
Dans une urne se trouvent 3 boules indiscernables au toucher numérotées de 1 à 3. Marie réalise l'experience aléatoire suivante. Elle tire au hasard trois boules dans l'urne avec remise, puis elle aditionne les trois numéros relevés.
1)Définir de manière ensembliste un univers oméga sur lequel il y a équiprobabilité. Dans ce but, on utilisera un arbre que l'on dessinera sur la copie.
2)On considère les évenèments suivants:
s:"obtenir une somme de 6" d:"le premier jeton tiré est pair"
a) Définir les évènement s et d de manière ensembliste
b) calculer les probabilité P(s) et P(d)
Faites ce que vous pouvez, merci d'avance.
DM sur les probabilités 2nde
3 messages
- Page 1 sur 1
[quote="auree2"]Bonjour j'ai un dm sur les probabilités, il y a un exercice que je n'arrive pas à faire:
Dans une urne se trouvent 3 boules indiscernables au toucher numérotées de 1 à 3. Marie réalise l'experience aléatoire suivante. Elle tire au hasard trois boules dans l'urne avec remise, puis elle aditionne les trois numéros relevés.
1)Définir de manière ensembliste un univers oméga sur lequel il y a équiprobabilité. Dans ce but, on utilisera un arbre que l'on dessinera sur la copie.
______/----1
/------1----2 puis encore un tirage
______\---3
-------2 pareil qu'en haut
\------3 idem
2)On considère les évenèments suivants:
s:"obtenir une somme de 6" d:"le premier jeton tiré est pair"
a) Définir les évènement s et d de manière ensembliste
b) calculer les probabilité P(s) et P(d)
P(d)=1/3(le premier tirage est 2).
P(s)=7/27 = nbre de tirage favorable/nbre de tirage possible
Faites ce que vous pouvez, merci d'avance.
Dans une urne se trouvent 3 boules indiscernables au toucher numérotées de 1 à 3. Marie réalise l'experience aléatoire suivante. Elle tire au hasard trois boules dans l'urne avec remise, puis elle aditionne les trois numéros relevés.
1)Définir de manière ensembliste un univers oméga sur lequel il y a équiprobabilité. Dans ce but, on utilisera un arbre que l'on dessinera sur la copie.
______/----1
/------1----2 puis encore un tirage
______\---3
-------2 pareil qu'en haut
\------3 idem
2)On considère les évenèments suivants:
s:"obtenir une somme de 6" d:"le premier jeton tiré est pair"
a) Définir les évènement s et d de manière ensembliste
b) calculer les probabilité P(s) et P(d)
P(d)=1/3(le premier tirage est 2).
P(s)=7/27 = nbre de tirage favorable/nbre de tirage possible
Faites ce que vous pouvez, merci d'avance.
(1,1,1),(1,1,2),(1,1,3);(1,2,1),(1,2,2),(1,2,3),(1,3,1),(1,3,2),(1,3,3)
(2,1,1),(2,1,2),(2,1,3),(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3)
(3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),(3,3,1),(3,3,2),(3,3,3)
chaque triplet correspond à une branche de l'arbre depuis la racine jusques aux feuilles,
la branche est pondérée à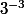
(2,1,1),(2,1,2),(2,1,3),(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3)
(3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),(3,3,1),(3,3,2),(3,3,3)
chaque triplet correspond à une branche de l'arbre depuis la racine jusques aux feuilles,
la branche est pondérée à
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
