[Tle S] DM Sur les fonctions

[black-whisper]

[FONT=Times New Roman]Bonjour, je bute sur quelques questions de mon devoir maison (assez difficile )
Question 1b) (eh oui les difficultés commencent vite)
g(x)=x³+6x-2 Demontrer que g(x)=0 a une seule solution sur puis donner son encadrement a (fait)
Justifier en particulier l'inégalité : |;)|<

Question 4)a) (entre autre on a eu une nouvelle fonction)
f(x)= (2x³-3x²-4)/(x²+2) J'ai calculé la dérivée f'(x)= qui m'a permis de dresser un tableau de variation de f sur .
Montrer que f(a)=3(a-1) puis en déduire que f(0)-f(;))=
Merci d'avance.
[/FONT]

[Lechero]

Salut !

Pour la 1-b), tu fais la dérivée + tableau de signe de g, et ensuite tu utilises le TVI (Théorème des Valeurs Intermédiaires) pour trouver la solution

[black-whisper]

Salut !

Pour la 1-b), tu fais la dérivée + tableau de signe de g, et ensuite tu utilises le TVI (Théorème des Valeurs Intermédiaires) pour trouver la solution

Merci mais je l'ai déja fait (tout ce qui est en vert)

[black-whisper]

J'ai apporté des modifications a l'enoncé tout en rajoutant des balises TEX

[black-whisper]

Up. S'il vous plait c'est pour Vendredi

[black-whisper]

Personne n'a trouvé?
Sur un autre forum on m'a posté

Bonsoir ,

Si tu as répondu à la question :

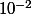
"Démontrer que g(x)=0 a une seule solution a sur R puis donner son encadrement à près."

Il doit être évident d'en déduire que .

Pour montrer que f()=3(-1) souviens-toi de la définition de et déduis-en que .

Bon courage.

Je n'ai pas trop compris la definition de

[Ericovitchi]

justifier que la racine est inférieure à 1/3 ?

tu sais que la fonction est croissante donc si tu montres que f(1/3) > 0 tu seras sûr que la racine est plus petite

f(a)=3(a-1)

tu sais que a est solution donc que a³+6a-2=0
f(a)=(2a³-3a²-4)/(a²+2) utilises la relation pour remplacer des a et bidouilles jusqu'à ce que tu trouves 3(a-1)

[black-whisper]

justifier que la racine est inférieure à 1/3 ?

tu sais que la fonction est croissante donc si tu montres que f(1/3) > 0 tu seras sûr que la racine est plus petite

Merci

f(a)=3(a-1)

tu sais que a est solution donc que a³+6a-2=0
f(a)=(2a³-3a²-4)/(a²+2) utilises la relation pour remplacer des a et bidouilles jusqu'à ce que tu trouves 3(a-1)

As tu vraiment trouvé la solution car j'ai essayé précedemment sans succès (je ne demande pas la réponse, ou du moins pas encore)

[Ericovitchi]

As tu vraiment trouvé la solution car j'ai essayé précedemment sans succès (je ne demande pas la réponse, ou du moins pas encore)

non j'ai vaguement essayé mais c'est vrai que l'on y arrive pas directement. J'ai laissé tombé.

[Mortelune]

J'ai trouvé la solution avec l'indication donnée par Ericovitchi c'est à dire le bidouillage.

Essaye peut être de partir de ce que tu dois obtenir pour voir qu'en enlevant ou ajoutant 0 le nombre de fois qu'il faut ça puisse te donner ce que tu cherches c'est à dire f(a)=3(a-1).

[black-whisper]

Le probleme reste d'inserer le denominateur (c'est bien celui du bas?)

Je suis pas le seul a m'être cassé les dents :cry:

[black-whisper]

Merci a tous ceux qui ont repondu j'ai trouvé il suffit de multiplier 3(a-1) par le denominateur et d'enlever une fois g(a) par contre j'ai des difficultés pour la question suivante

: puis en déduire f(0)-f(a)=

[black-whisper]

Bon les cerveaux peuvent se reposer j'ai trouvé.^^

Euh parlé trop vite :/

Ben si finalement^^

[black-whisper]

Je me demande comment |f(0)-f(;))|< pourrait avoir une conséquence sur la courbe représentative de f(x).

...a moins que ce soit f(0)-f(;))= qui puisse y faire quelque chose

[black-whisper]

Personne :s.