Je bloque sur un exo:
Soit f la fonction définie sur [-4 ; 5] par f (x)= 2x+1/x²+2; on note C sa courbe représentative dans le plan rapporté à un repère orthogonal (unités graphiques: 1cm en abscisse et 3 cm en ordonnée).
1. Déterminer les coordonnées du point d'intersection I1 de C avec l'axe des abscisses.
(-1,5 ; 0) mais je ne sais pas comment le montrer par un calcul.
2. Déterminer les coordonnées du point d'intersection I2 de C avec l'axe des ordonnées.
(0 ; 6) idem qu'avant
3. Calculer f ' (x).
u(x)= 2x+1 u' (x)=2*1+0=2
v(x)=x²+2 v' (x)=2x+0=2x
2(x²+2)-(2x+1)2x/(x²+2)² = 2x²+4-4x²-2x/(x²+2)² = -2x²-2x+4/(x²+2)²
4. a) Développer -2(x+2) (x-1).
-2 (x²-1x+2x-2) = -2x²+2x-4x+4 = -2x²-2x+4
b) Etudier le signe de -2x²-2x+4.
-2*2x-2*1+0=-4x-2
f(x)>0 <=>-4x-2>0
<=>2>4x
<=>2/4>x
car a>0
c) En déduire le signe de f'(x), puis le sens de variation de f. Dresser son tableau de variation, en précisant les éventuels extremums locaux.
Ceci, je n'arrive pas.
5. Tracer C.
6. Résoudre l'équation f (x)=1 ; vérifier graphiquement le résultat.
2x+1/x²+2=1
7. Résoudre l'inéquation f( x) >1 ; vérifier graphiquement le résultat.
2x+1/x²+2>1
Merci de bien vouloir m'aider :we:
DM: sur les fonctions dérivées (niveau term)
14 messages
- Page 1 sur 1
En fait pour trouver, du point de vue général, l'intersection de deux courbes, on est amené à résoudre un systeme d'équation. Par exemple, prenons  vers
vers  représentées par
représentées par  le point d'intersection de }C_1 \quad et C_2)
alors on peut écrire que x et y vérifient :=y \atop f_2(x)=y}\right)
Du coup ca t'amene à résoudre un systeme. Par exemple dans le cas ou tu veux l'intersection de C et (Ox), tu peux considerer comme f et
comme f et 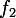 comme g : R vers R qui a x associe 0.
comme g : R vers R qui a x associe 0.
A toi de jouer pour ces 2 premieres questions^^
alors on peut écrire que x et y vérifient :
Du coup ca t'amene à résoudre un systeme. Par exemple dans le cas ou tu veux l'intersection de C et (Ox), tu peux considerer
A toi de jouer pour ces 2 premieres questions^^
pour la question 4.c) est ce qu'il faut mettre au même dénominateur:
x²+2/x²+2*x²+2*(-2x²-2x+4)/(x²+2) ou il faut faire autrement pour trouver le signe de f ' (x)
f ' (x) >0
<=> x²+2*(-2x²-2x+4)
pour la question 6.:
2x+1/x²+2=1
2x+1=1(x²+2)
2x+1=1x²+2
2x+1-1=1x²+2-1
2x/2=1x²+1/2
x=1x²+1/2
pour la question 7.:
2x+1/x²+2>1
2x+1=1 x²+2=1
2x+1-1=1-1 x²+2-2=1-2
2x/2=0/2 x²=-1
x=0 x=-1
Merci de me venir en aide :help:
x²+2/x²+2*x²+2*(-2x²-2x+4)/(x²+2) ou il faut faire autrement pour trouver le signe de f ' (x)
f ' (x) >0
<=> x²+2*(-2x²-2x+4)
pour la question 6.:
2x+1/x²+2=1
2x+1=1(x²+2)
2x+1=1x²+2
2x+1-1=1x²+2-1
2x/2=1x²+1/2
x=1x²+1/2
pour la question 7.:
2x+1/x²+2>1
2x+1=1 x²+2=1
2x+1-1=1-1 x²+2-2=1-2
2x/2=0/2 x²=-1
x=0 x=-1
Merci de me venir en aide :help:
Bonsoir, alors pour la 1ere question, voici une demarche assez générale :
L'intersection entre C et (Ox) est le point (x,y) qui vérifie f(x)=y et y=0 ( l'axe des abscisses ), c'est à dire le point qui appartient aux deux courbes, on peut donc traduire ceci par un systeme :
=\frac{2x+1}{x^2+2}=y \atop y=0}\right)
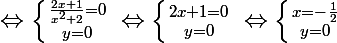 .
.
Donc le point I a pour coordonner (-0.5,0).
A toi d'adapter pour la question 2.
L'intersection entre C et (Ox) est le point (x,y) qui vérifie f(x)=y et y=0 ( l'axe des abscisses ), c'est à dire le point qui appartient aux deux courbes, on peut donc traduire ceci par un systeme :
Donc le point I a pour coordonner (-0.5,0).
A toi d'adapter pour la question 2.
Ensuite pour ta question 4),
tu as pu remarquer que le numérateur de f' était la meme expression qu'on t'a demandé de développer et d'étudier le signe ?
D'ailleurs comment fais-tu pour trouver le signe de -2x²-2x+4 ?
Une fois que tu auras bien déterminé le signe de -2x²-2x+4, que peux tu dire du signe de f' ? En quoi ca t'aide d'avoir trouver le signe de -2x²-2x+4 ?
tu as pu remarquer que le numérateur de f' était la meme expression qu'on t'a demandé de développer et d'étudier le signe ?
D'ailleurs comment fais-tu pour trouver le signe de -2x²-2x+4 ?
Une fois que tu auras bien déterminé le signe de -2x²-2x+4, que peux tu dire du signe de f' ? En quoi ca t'aide d'avoir trouver le signe de -2x²-2x+4 ?
Encore une aide pour les réponses suivantes,
Pour la 6), on te demande de résoudre sur [-4;5], f(x)=1,
Procédons par équivalence :
=1 \Longleftrightarrow \frac{2x+1}{x^2+2} = 1 \Longleftrightarrow \frac{2x+1}{x^2+2}-\frac{x^2+2}{x^2+2} = 0 \Longleftrightarrow \text{??}) .
.
A toi de nous dire pour la suite, tu devrais arriver à quelque chose de simple et que tu sais bien résoudre.
Il en va de meme pour la question 7) sauf que tu dois résoudre non pas une équation mais une inéquation.
Ok ?
Pour la 6), on te demande de résoudre sur [-4;5], f(x)=1,
Procédons par équivalence :
A toi de nous dire pour la suite, tu devrais arriver à quelque chose de simple et que tu sais bien résoudre.
Il en va de meme pour la question 7) sauf que tu dois résoudre non pas une équation mais une inéquation.
Ok ?
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
