Sujet spécial Bac 2009
Bon alors voilà, exo 1 question 2 (b) j'initialise à  et
et  donc c'est ok pour le rang 0.
donc c'est ok pour le rang 0.
Donc au rang n j'ai . Je check le rang (n+1) ça fait
. Je check le rang (n+1) ça fait  et je pose
et je pose  différent de 0 et après des calculs je tombe sur
différent de 0 et après des calculs je tombe sur  et donc
et donc  .
.
Prop init en 0 et héréditaire donc je pense que c'est ok.
Et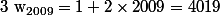
J'espère que j'ai pas fait de fautes en tapant.
 et
et  donc c'est ok pour le rang 0.
donc c'est ok pour le rang 0.Donc au rang n j'ai
 . Je check le rang (n+1) ça fait
. Je check le rang (n+1) ça fait  et je pose
et je pose  différent de 0 et après des calculs je tombe sur
différent de 0 et après des calculs je tombe sur  et donc
et donc  .
.Prop init en 0 et héréditaire donc je pense que c'est ok.
Et
J'espère que j'ai pas fait de fautes en tapant.
Exo 2 partie 1 question (1) c'est du cours : la lim en + l'infini de  c'est la même que celle de
c'est la même que celle de  et c'est 0 car
et c'est 0 car  (trop long le LaTeX :mur:) et donc je tombe sur lim en plus l'inf de (1+xe^{-x})=1 et comme la lim en 1 de log de x ça vaut 0, si je compose les deux j'ai deux limites en 0 donc j'ai ma réponse.
(trop long le LaTeX :mur:) et donc je tombe sur lim en plus l'inf de (1+xe^{-x})=1 et comme la lim en 1 de log de x ça vaut 0, si je compose les deux j'ai deux limites en 0 donc j'ai ma réponse.
Pour la (2) f est dérivable sur [0, + inf[ et ça donne et vu que dans les positifs x est sup ou égale à 0 et e^-x est strictement sup à 0 on a
et vu que dans les positifs x est sup ou égale à 0 et e^-x est strictement sup à 0 on a  et donc voilà.
et donc voilà.
Bon la (3) c'est facile aussi je pense, sur [0,1] je trouve f'(x) pos donc f croissante (principe de je ne sais plus qui) et sur ]1, + inf[ f'(x) neg donc f décroissante. Avant j'ai étudié la valeur de x dans x-1 suivant que ce soit pos, neg ou nul.
EDIT : mon dieu que c'est brouillon :O
EDIT 2 : oh non des int dans la partie 2
 c'est la même que celle de
c'est la même que celle de  et c'est 0 car
et c'est 0 car  (trop long le LaTeX :mur:) et donc je tombe sur lim en plus l'inf de (1+xe^{-x})=1 et comme la lim en 1 de log de x ça vaut 0, si je compose les deux j'ai deux limites en 0 donc j'ai ma réponse.
(trop long le LaTeX :mur:) et donc je tombe sur lim en plus l'inf de (1+xe^{-x})=1 et comme la lim en 1 de log de x ça vaut 0, si je compose les deux j'ai deux limites en 0 donc j'ai ma réponse.Pour la (2) f est dérivable sur [0, + inf[ et ça donne
 et vu que dans les positifs x est sup ou égale à 0 et e^-x est strictement sup à 0 on a
et vu que dans les positifs x est sup ou égale à 0 et e^-x est strictement sup à 0 on a  et donc voilà.
et donc voilà.Bon la (3) c'est facile aussi je pense, sur [0,1] je trouve f'(x) pos donc f croissante (principe de je ne sais plus qui) et sur ]1, + inf[ f'(x) neg donc f décroissante. Avant j'ai étudié la valeur de x dans x-1 suivant que ce soit pos, neg ou nul.
EDIT : mon dieu que c'est brouillon :O
EDIT 2 : oh non des int dans la partie 2
Timothé Lefebvre a écrit:Exo 2 partie 1 question (1) c'est du cours : la lim en + l'infini dec'est la même que celle de
et c'est 0 car
(trop long le LaTeX :mur:) et donc je tombe sur lim en plus l'inf de (1+xe^{-x})=1 et comme la lim en + l'inf de log de x ça vaut 0, si je compose les deux j'ai deux limites en 0 donc j'ai ma réponse.
en 1 plutôt
Partie 2 : je connais mal les intégrales  j'essaye quand même mais ça va être très mauvais.
j'essaye quand même mais ça va être très mauvais.
Question 1 (a) ça va je prends la partie sous la courbe et "bloquée" par l'abscisse . Après la (b) en me servant l'énoncé je peut argué (sans être convaincu le moins du monde) que l'encadrement qu'ils donnent je pense que ça doit être en rapport avec l'aire du recatngle de dim
. Après la (b) en me servant l'énoncé je peut argué (sans être convaincu le moins du monde) que l'encadrement qu'ils donnent je pense que ça doit être en rapport avec l'aire du recatngle de dim  et f(1).
et f(1).
Pour la 2, (a) je pose et
et  et je calcule leurs dérivées parce que je sais qu'il faut faire comme ça mais après je me perds dans mes calculs ...
et je calcule leurs dérivées parce que je sais qu'il faut faire comme ça mais après je me perds dans mes calculs ...
Pour la (b) c'est plus facile ça nous donne : sur [0,+inf[ j'ai xe^{-x} est strictement pos donc inférieur ou égale à
inférieur ou égale à  et des deux fn sont continues sur [0,+inf[ et donc la je fais un passage périlleux par mes amies intégrales (ironie) et j'ai
et des deux fn sont continues sur [0,+inf[ et donc la je fais un passage périlleux par mes amies intégrales (ironie) et j'ai  et là je bloque aussi.
et là je bloque aussi.
Bref les intégrales j'aime pas (pas trop) !
Pour la 3 fastoche et ça donne
et ça donne  et après j'utilise le résultat que je n'ai pas retouvé (merci l'énoncé de me permettre de continuer quand même !) et donc
et après j'utilise le résultat que je n'ai pas retouvé (merci l'énoncé de me permettre de continuer quand même !) et donc  et donc
et donc  euhhh la deuxième a donc l'air meilleure non ?
euhhh la deuxième a donc l'air meilleure non ?
Je m'attaque à la suite !
EDIT : OH ! Une ROC !! Je croyais qu'il y en aurait pas !
Question 1 (a) ça va je prends la partie sous la courbe et "bloquée" par l'abscisse
 . Après la (b) en me servant l'énoncé je peut argué (sans être convaincu le moins du monde) que l'encadrement qu'ils donnent je pense que ça doit être en rapport avec l'aire du recatngle de dim
. Après la (b) en me servant l'énoncé je peut argué (sans être convaincu le moins du monde) que l'encadrement qu'ils donnent je pense que ça doit être en rapport avec l'aire du recatngle de dim  et f(1).
et f(1).Pour la 2, (a) je pose
 et
et  et je calcule leurs dérivées parce que je sais qu'il faut faire comme ça mais après je me perds dans mes calculs ...
et je calcule leurs dérivées parce que je sais qu'il faut faire comme ça mais après je me perds dans mes calculs ... Pour la (b) c'est plus facile ça nous donne : sur [0,+inf[ j'ai xe^{-x} est strictement pos donc
 inférieur ou égale à
inférieur ou égale à  et des deux fn sont continues sur [0,+inf[ et donc la je fais un passage périlleux par mes amies intégrales (ironie) et j'ai
et des deux fn sont continues sur [0,+inf[ et donc la je fais un passage périlleux par mes amies intégrales (ironie) et j'ai  et là je bloque aussi.
et là je bloque aussi.Bref les intégrales j'aime pas (pas trop) !
Pour la 3 fastoche
 et ça donne
et ça donne  et après j'utilise le résultat que je n'ai pas retouvé (merci l'énoncé de me permettre de continuer quand même !) et donc
et après j'utilise le résultat que je n'ai pas retouvé (merci l'énoncé de me permettre de continuer quand même !) et donc  et donc
et donc  euhhh la deuxième a donc l'air meilleure non ?
euhhh la deuxième a donc l'air meilleure non ?Je m'attaque à la suite !
EDIT : OH ! Une ROC !! Je croyais qu'il y en aurait pas !
Alors exo 3 (1) (ils sont gentils ils te donnent même le cours au cas où tu aies oublié de le rentrer dans ta calto ... même la formule des combinaisons ! c'est décidé j'apprends plus rien !) donc j'utilise leur rappel pour calcul  et
et  donc après j'additonne tout et après de multiples calculs (ma foi très brouillons) et je tombe sur
donc après j'additonne tout et après de multiples calculs (ma foi très brouillons) et je tombe sur  de là je simplifie et j'ai
de là je simplifie et j'ai  tels que
tels que  . (J'aurais pensé utiliser Pascal ?).
. (J'aurais pensé utiliser Pascal ?).
Partie 2 des probas enfin des vraies. Alors 1 (a) (euhh du dénombrement ...) j'ai mis
enfin des vraies. Alors 1 (a) (euhh du dénombrement ...) j'ai mis  et pour l'autre
et pour l'autre  et donc pour les deux jetons blancs je fais le quotient 21/45 qui donne 7/15.
et donc pour les deux jetons blancs je fais le quotient 21/45 qui donne 7/15.
Pour le (b) j'ai aussi 45 poss pour 2 jetons et pour 2 impairs vu que j'en 6 j'ai et bla bla bla même motif même punition (comme dit Domi lol) quotient, je trouve 1/3.
et bla bla bla même motif même punition (comme dit Domi lol) quotient, je trouve 1/3.
Pour le (c) on vaire un peu les plaisirs, passons aux évènement indépendants Je cite la def P(A inter B)=P(A)*P(B) ensuite j'applique (ce que j'ai calculé mais je ne l'écris pas là, trop long !) P(A intr B) =
Je cite la def P(A inter B)=P(A)*P(B) ensuite j'applique (ce que j'ai calculé mais je ne l'écris pas là, trop long !) P(A intr B) =  et je compare après avec P(A)*P(B) qui vaut (7/15)*(1/3)=7/45 surprise ils sont différents donc pas indépendants.
et je compare après avec P(A)*P(B) qui vaut (7/15)*(1/3)=7/45 surprise ils sont différents donc pas indépendants.
Question 2 du classique (comme si on s'y attendait pas tiens !). X peut prendre 3 valeurs : 0,1 ou 2. Etude de cas. X=0 on doit tirer 2 noirs donc pour X=1 je trouve
pour X=1 je trouve  et pareil pour X=2 et donc P(X=2). Bon après je pose le tableau.
et pareil pour X=2 et donc P(X=2). Bon après je pose le tableau.
Pour (b) bon bah là je somme comme le cours le dit et je trouve 7/5.
Je suis sûr que j'ai fait pleins de fautes, je relis et je passe au 4(spé) !
 et
et  donc après j'additonne tout et après de multiples calculs (ma foi très brouillons) et je tombe sur
donc après j'additonne tout et après de multiples calculs (ma foi très brouillons) et je tombe sur  de là je simplifie et j'ai
de là je simplifie et j'ai  tels que
tels que  . (J'aurais pensé utiliser Pascal ?).
. (J'aurais pensé utiliser Pascal ?).Partie 2 des probas
 et pour l'autre
et pour l'autre  et donc pour les deux jetons blancs je fais le quotient 21/45 qui donne 7/15.
et donc pour les deux jetons blancs je fais le quotient 21/45 qui donne 7/15.Pour le (b) j'ai aussi 45 poss pour 2 jetons et pour 2 impairs vu que j'en 6 j'ai
 et bla bla bla même motif même punition (comme dit Domi lol) quotient, je trouve 1/3.
et bla bla bla même motif même punition (comme dit Domi lol) quotient, je trouve 1/3.Pour le (c) on vaire un peu les plaisirs, passons aux évènement indépendants
 et je compare après avec P(A)*P(B) qui vaut (7/15)*(1/3)=7/45 surprise ils sont différents donc pas indépendants.
et je compare après avec P(A)*P(B) qui vaut (7/15)*(1/3)=7/45 surprise ils sont différents donc pas indépendants.Question 2 du classique (comme si on s'y attendait pas tiens !). X peut prendre 3 valeurs : 0,1 ou 2. Etude de cas. X=0 on doit tirer 2 noirs donc
 pour X=1 je trouve
pour X=1 je trouve  et pareil pour X=2 et donc P(X=2). Bon après je pose le tableau.
et pareil pour X=2 et donc P(X=2). Bon après je pose le tableau.Pour (b) bon bah là je somme comme le cours le dit et je trouve 7/5.
Je suis sûr que j'ai fait pleins de fautes, je relis et je passe au 4(spé) !
Exo 4 (celui de spé). Pour la 1 (a) on a déjà bien entendu (1,1) comme solution. Ensuite on pose 8x-5y=3 et donc
8(x-1)=5(y-1). 8 et 5 sont prem's entre eux donc on utilise Gauss et je trouve y=8k+1 et x=5k+1. Pour tout k relatif on a le couple (5k+1,8k+1) qui est solution de (E). Donc l'ensemble de solution de (E) est {(5k+1,8k+1);k dans Z}.
La (b), si un tel m existe alors 8p-5q=3 et donc (p,q) est bien solution. Et comme c'est bien le cas il existe un k tel que p=5k+1 donc 8p et 8 congrus modulo 40 et m et 0 congrus modulo 40.
(c) : 2009 et 9 congurs modulo 40 donc le plus petit m sup à 2000 est 2009.
Question 2 (a) : 2^3=8 et 2^3 et 1 congrus modulo 7 donc 2^{3k} et 1^k congrus modulo 7.
On a 2009 : 3*669+2 donc 2^2009 = 2^{3*669}*2² après je me sers de ce que j'ai montré ci-dessus et je tombe sur 2^2009 et 4 congrus modulo 7 donc le reste de la d.e de 2^2009 par 7 est 4.
Question 3 ca se complique. (a) j'ai 10 et 3 congrus modulo 7 donc 10^3 et 27 congrus modulo 7 et donc 1O^3 et -1 congrus modulo 7.
Pour la (b) j'ai pas encore fini mais en gros N est divisible par 7 donc N et 0 congrus modulo 7 j'ai trouvé un trud du genre N et (b-a) congrus modulo 7. Je vais faire une étude de cas.
8(x-1)=5(y-1). 8 et 5 sont prem's entre eux donc on utilise Gauss et je trouve y=8k+1 et x=5k+1. Pour tout k relatif on a le couple (5k+1,8k+1) qui est solution de (E). Donc l'ensemble de solution de (E) est {(5k+1,8k+1);k dans Z}.
La (b), si un tel m existe alors 8p-5q=3 et donc (p,q) est bien solution. Et comme c'est bien le cas il existe un k tel que p=5k+1 donc 8p et 8 congrus modulo 40 et m et 0 congrus modulo 40.
(c) : 2009 et 9 congurs modulo 40 donc le plus petit m sup à 2000 est 2009.
Question 2 (a) : 2^3=8 et 2^3 et 1 congrus modulo 7 donc 2^{3k} et 1^k congrus modulo 7.
On a 2009 : 3*669+2 donc 2^2009 = 2^{3*669}*2² après je me sers de ce que j'ai montré ci-dessus et je tombe sur 2^2009 et 4 congrus modulo 7 donc le reste de la d.e de 2^2009 par 7 est 4.
Question 3 ca se complique. (a) j'ai 10 et 3 congrus modulo 7 donc 10^3 et 27 congrus modulo 7 et donc 1O^3 et -1 congrus modulo 7.
Pour la (b) j'ai pas encore fini mais en gros N est divisible par 7 donc N et 0 congrus modulo 7 j'ai trouvé un trud du genre N et (b-a) congrus modulo 7. Je vais faire une étude de cas.
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

