Un sujet modifiée : Demonstration dans Z
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 23 Fév 2019, 22:43
par zerow2001 » 23 Fév 2019, 22:43
Salut tout le monde !
la question est :
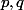
sont deux nombres premiers et différents.
et n = pq
Montrez que pour :
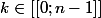
=1 \Leftrightarrow \begin{cases}<br /> & \text{ } p *k \\ <br /> & \text{ et } q*k <br />\end{cases})
* : ne divise pas
on doit montrer que p ne divise pas k et q ne divise pas k.
merci !!!

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 23 Fév 2019, 23:15
par Lostounet » 23 Fév 2019, 23:15
Salut
Bon tu avais oublié n=pq quand même !
Sinon l'exercice n'est pas intéressant. Il n'y a presque rien à montrer.
Tu as fait quoi ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 23 Fév 2019, 23:21
par zerow2001 » 23 Fév 2019, 23:21
j'ai dit : n*k alors pq*k et je crois pas que je peux conclure que a*k et q*k si p et premier et q est premier
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 24 Fév 2019, 10:25
par pascal16 » 24 Fév 2019, 10:25
pq*k si k ne vaut pas 1, pq*k > n
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 24 Fév 2019, 11:06
par zerow2001 » 24 Fév 2019, 11:06
pascal16 a écrit:pq*k si k ne vaut pas 1, pq*k > n
j'ai pas bien compris

-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 24 Fév 2019, 11:16
par zerow2001 » 24 Fév 2019, 11:16
est ce qu'on peut dire : puisque k n'as pas un diviseur commun avec n, et n = pq, alors p et q ne peuvent pas diviser k ?
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 24 Fév 2019, 11:36
par zerow2001 » 24 Fév 2019, 11:36
j'ai répondu, il est facile, desolé pour le dérangement
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
