Suites : Trouver une relation de récurrence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 29 Avr 2013, 09:49
par upium666 » 29 Avr 2013, 09:49
Bonjour à tous et à toutes
_{ n \in \mathbb{N}^* })
une suite (dont on ne connaît pas encore la nature)
Elle se construit comme suit :
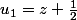
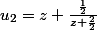
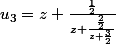
...
Exprimer la suite à l'aide d'une relation de récurrence
(C'est une première étape, cela me servira pour autre chose, mais je n'y arrive pas encore :hein: )
Merci de m'aider !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 30 Avr 2013, 09:41
par Kikoo <3 Bieber » 30 Avr 2013, 09:41
upium666 a écrit:Bonjour à tous et à toutes
_{ n \in \mathbb{N}^* })
une suite (dont on ne connaît pas encore la nature)
Elle se construit comme suit :
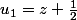
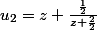
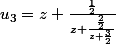
...
Exprimer la suite à l'aide d'une relation de récurrence
(C'est une première étape, cela me servira pour autre chose, mais je n'y arrive pas encore :hein: )
Merci de m'aider !
Salut,
On voit que l'on a
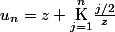
et qu'alors par un petit tour de magie,
(z+\frac{n+1}{2})}{z\(z+ \frac{n+1}{2}\)+ \frac{n}{2}}})
Sauf erreur.
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 02 Mai 2013, 00:04
par upium666 » 02 Mai 2013, 00:04
Kikoo <3 Bieber a écrit:Salut,
On voit que l'on a
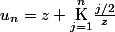
et qu'alors par un petit tour de magie,
(z+\frac{n+1}{2})}{z\(z+ \frac{n+1}{2}\)+ \frac{n}{2}}})
Sauf erreur.
Merci beaucoup Kikoo (je suis en train de vérifier)
Maintenant que c'est fait je vous invite à suivre une discussion que j'ouvrirai prochainement, les 2 étapes qui me restent sont les suivantes :
1)Exprimer

en fonction de

2)Trouver

(qui, croyez-moi, existe :lol3: )
Vous en verrez l'utilité si on y arrive :we:
Cordialement :happy2:
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 02 Mai 2013, 08:50
par Kikoo <3 Bieber » 02 Mai 2013, 08:50
Si mon calcul est juste, il faut réarranger sous une forme potable (suite arithmético-géométrique) :
\(z+\frac{n+1}{2}\)}{z\(z+ \frac{n+1}{2}\)+ \frac{n}{2}}}\\<br />=z\(1-\frac{z\(z+ \frac{n+1}{2}\)+ \frac{n}{2}}{\(z+\frac{n}{2}\)\(z+\frac{n+1}{2}\)}\)+ \frac{z\(z+ \frac{n+1}{2}\)+ \frac{n}{2}}{\(z+\frac{n}{2}\)\(z+\frac{n+1}{2}\)} u_n=b+au_n)
Or a=1 ssi
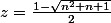
ou
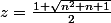
Donc pour de telles valeurs de z, nous avons
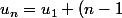b=u_1=z+\frac{1}{2})
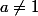
sinon, et alors :
+ \frac{n}{2}}{\(z+\frac{n}{2}\)\(z+\frac{n+1}{2}\)}\)^{n-1}\(u_1-\frac{z\(1-\frac{z\(z+ \frac{n+1}{2}\)+ \frac{n}{2}}{\(z+\frac{n}{2}\)\(z+\frac{n+1}{2}\)}\)}{1-\frac{z\(z+ \frac{n+1}{2}\)+ \frac{n}{2}}{\(z+\frac{n}{2}\)\(z+\frac{n+1}{2}\)}}\)+\frac{z\(1-\frac{z\(z+ \frac{n+1}{2}\)+ \frac{n}{2}}{\(z+\frac{n}{2}\)\(z+\frac{n+1}{2}\)}\)}{1-\frac{z\(z+ \frac{n+1}{2}\)+ \frac{n}{2}}{\(z+\frac{n}{2}\)\(z+\frac{n+1}{2}\)}}) <<<< plus grosse expression ever (à simplifier en...) :
<<<< plus grosse expression ever (à simplifier en...) :+ \frac{n}{2}}{\(z+\frac{n}{2}\)\(z+\frac{n+1}{2}\)}\)^{n-1}\(u_1-z\)+z)
Et pour n tendant vers plus l'infini... On obtient

?
Bon, je laisse les calculs jusqu'à ce que quelqu'un me dise si j'ai fait faux ou non :doh:
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
 par Archytas » 03 Mai 2013, 19:44
par Archytas » 03 Mai 2013, 19:44
upium, où trouves-tu ces énoncés ?
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 07 Mai 2013, 12:45
par upium666 » 07 Mai 2013, 12:45
Archytas a écrit:upium, où trouves-tu ces énoncés ?
Dans mes pensées ... :ptdr:
Je pense souvent des énoncés pour pouvoir arriver à certains objectifs, une sorte de "travail de recherche" d'amateur (bien que je n'aime pas employer le terme "recherche" que je ne réserve qu'aux grands de ce monde !)
Ce qui m'a poussé à définir cet énoncé est la recherche d'une expression de la fonction d'erreur ...
(c.f :
http://www.maths-forum.com/integrale-gauss-140863.php )
:lol3:
(Et si on y arrive, chose très improbable, ... :we: )
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
 par Archytas » 07 Mai 2013, 18:51
par Archytas » 07 Mai 2013, 18:51
upium666 a écrit:Dans mes pensées ... :ptdr:
Je pense souvent des énoncés pour pouvoir arriver à certains objectifs, une sorte de "travail de recherche" d'amateur (bien que je n'aime pas employer le terme "recherche" que je ne réserve qu'aux grands de ce monde !)
Ce qui m'a poussé à définir cet énoncé est la recherche d'une expression de la fonction d'erreur ...
(c.f :
http://www.maths-forum.com/integrale-gauss-140863.php )
:lol3:
(Et si on y arrive, chose très improbable, ... :we: )
D'accord, très bien ! Continu comme ça.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
une suite (dont on ne connaît pas encore la nature)
et qu'alors par un petit tour de magie,