Suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
stef78
- Membre Relatif
- Messages: 142
- Enregistré le: 18 Mai 2006, 16:57
-
 par stef78 » 10 Oct 2006, 18:29
par stef78 » 10 Oct 2006, 18:29
bonjour,
la suite u est definie par:
Uo=-1 et pour tout entier naturel n
Un+1= (1/2)Un + n
Calculer U1,U2;U3
je trouve U1= 1/2Uo + 0 = -0.5
U2= 1/2U1 +1 = 0.75
et U3= 1/2U2 +2 = 2.375
et
Vn= Un -2n + 4
demontrer que v est une suite geometrique
je fais donc Vn+1= U(n+1) - 2n + 1 + 4
= 1/2Un + n - 2n + 5
= 1/2Un - n + 2
dc 1/2(Un-2n+4)
d'autre part il me demande d'exprimer Un en fonction de n
on a donc:
Un= Vn +2n -4 ?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 10 Oct 2006, 18:40
par fonfon » 10 Oct 2006, 18:40
Salut, oui tu peut continuer
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 10 Oct 2006, 18:44
par fonfon » 10 Oct 2006, 18:44
Salut,
je fais donc Vn+1= U(n+1) - 2n + 1 + 4
je crois qu'il y a une petite erreur car u(n+1)-2(n+1)+4
-
stef78
- Membre Relatif
- Messages: 142
- Enregistré le: 18 Mai 2006, 16:57
-
 par stef78 » 10 Oct 2006, 18:50
par stef78 » 10 Oct 2006, 18:50
non j'ai juste oublié les parenthese dsl mais je les calculé sans erreur je crois, sur ma feuille je les avais mises
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 10 Oct 2006, 18:54
par fonfon » 10 Oct 2006, 18:54
oui, j'avais vu la suite et je m'en suis douté par contre pour un tu peux continuer c'est ok
-
stef78
- Membre Relatif
- Messages: 142
- Enregistré le: 18 Mai 2006, 16:57
-
 par stef78 » 10 Oct 2006, 18:55
par stef78 » 10 Oct 2006, 18:55
comment faire pour la suite ?on doit remplacer Vn par Voq^n mai ici le premier terme c'est V1 non ? car pr calculer Vo
il faut Uo-1
car Un+1= 1/2Un+n
-
ines001
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Avr 2006, 19:41
-
 par ines001 » 10 Oct 2006, 19:01
par ines001 » 10 Oct 2006, 19:01
bonjour,
Pour la première partie, juste une remarque, tu devrais mettre tes nombres decimaux sous forme de fraction à savoir -1/2 ; 3/4 et 19/8
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 10 Oct 2006, 19:03
par fonfon » 10 Oct 2006, 19:03
re,
tu viens de montrer que

donc la suite

est geometrique de raison 1/2 et de 1er terme

donc

s'ecrit ....
-
stef78
- Membre Relatif
- Messages: 142
- Enregistré le: 18 Mai 2006, 16:57
-
 par stef78 » 10 Oct 2006, 19:06
par stef78 » 10 Oct 2006, 19:06
Vn=3(1/2)^n + 2n-4 ?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 10 Oct 2006, 19:12
par fonfon » 10 Oct 2006, 19:12
Re, non il faut que tu reviennes à la definition d'une suite geometrique:
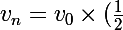^n=...)
et ensuite tu remplaces pour trouver

-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 10 Oct 2006, 19:13
par fonfon » 10 Oct 2006, 19:13
re,
Vn=3(1/2)^n + 2n-4 ?
ici ça serait pas plutôt Un
-
stef78
- Membre Relatif
- Messages: 142
- Enregistré le: 18 Mai 2006, 16:57
-
 par stef78 » 10 Oct 2006, 19:14
par stef78 » 10 Oct 2006, 19:14
ui dsl , c'est bon donc?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 10 Oct 2006, 19:15
par fonfon » 10 Oct 2006, 19:15
ben si c'est Un c'est bon alors
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
