Suites TS

par **pucinette17** » 11 Sep 2006, 11:31

bonjour a tous je n'arrive pas a étudier la monotonie d'une suite
j'essaye de faire la différence entre Un et U(n+1) mais je n'arrive pas a continuer mon calcul
dans mon exo j'ai trouvé que Un=11*(4/5)^n-5 et que U(n+1)=(4/5)Un-1
merci d'avance

par **nox** » 11 Sep 2006, 12:06

c'est quoi l'énoncé exact ?

par **Flodelarab** » 11 Sep 2006, 12:46

Moi je dirais plutot que U(n+i)=(4/5)^i Un - i

aux vues de ce que tu nous donnes ...

par **nox** » 11 Sep 2006, 12:51

Wai :++: ...mais de toute facon c'est juste U(n+1)=(4/5) Un - 1 qui nous intéresse...et la on voit bien que c'est décroissant quand meme...on multiplie par un truc inférieur à 1 et on soustrait un truc positif

par **Flodelarab** » 11 Sep 2006, 13:02

nox a écrit:Wai :++: ...mais de toute facon c'est juste U(n+1)=(4/5) Un - 1 qui nous intéresse...et la on voit bien que c'est décroissant quand meme...on multiplie par un truc inférieur à 1 et on soustrait un truc positif

histoire de traduire avec du latex:

par **nox** » 11 Sep 2006, 13:07

vouala ! là ca me parait optimal

par **rene38** » 11 Sep 2006, 13:21

Bonjour

Flodelarab a écrit:

Il serait peut-être utile de prouver que

pour tout naturel

.

par **nox** » 11 Sep 2006, 13:22

ah oui exact ! n'oublions pas ce détail qui n'en est pas un !
ca peut effectivement être utile

par **B_J** » 11 Sep 2006, 13:23

non
la monotonie ne depend pas du signe

par **Flodelarab** » 11 Sep 2006, 13:26

B_J a écrit:non
la monotonie ne depend pas du signe

du signe de koi ?

par **B_J** » 11 Sep 2006, 13:30

du terme

la suite

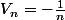
est bien monotone

par **nox** » 11 Sep 2006, 13:30

ce passage ne marche plus sinon

Flodelarab a écrit:

Un = -1

---> Faux

par **B_J** » 11 Sep 2006, 13:32

ok
desolé

par **nox** » 11 Sep 2006, 13:33

j'en ai fait des pires ^^

par **B_J** » 11 Sep 2006, 13:37

donc je supprime le message pour ne pas embrouiller les autres

par **nox** » 11 Sep 2006, 13:41

ba si tu veux mais je trouve que c'est bien ca permet d'avoir un contre exemple et d'expliquer le post de rene38

mais si tu preferes je reformule le mien

par **B_J** » 11 Sep 2006, 13:49

en tout cas c'est vrai que la monotonie d'une suite ne depend pas de son signe , mais dans ta demonstration il est necessaire de montrer que

par **nox** » 11 Sep 2006, 13:51

ba je comprends pas ce que tu veux dire par "la monotonie ne dépend pas du signe"...là on voit bien que c'est le cas non ?

par **B_J** » 11 Sep 2006, 13:55

je voulais dire qu'il existe des suites non positives qui sont monotones ( ex : -

)

par **nox** » 11 Sep 2006, 13:57

ah oui oki ^^

bien evidemment le fait qu'elle soit positive n'est pas une condition nécessaire et suffisante pour qu'elle soit croissante ou décroissante, ou même monotone (ni nécessaire ni suffisante)

on est donc d'accord

Suites TS

suites TS

Qui est en ligne