Suites

par **axouten** » 28 Mar 2010, 15:52

Bonjour à tous,

J'ai un DM de maths sur les suites et il y a une question que je ne comprends pas. Je vous donne le début de l'exercice pour que vous compreniez mieux :

On considère (Un) = 2n(en exposant) + n -1
et (Vn) = 2n(en exposant) - n +1

Calculer U0, U1, U2,U3 je trouve dans l'ordre 1, 2, 5, 10
Calculer V0, V1, V2, V3 je trouve dans l'ordre 3, 2, 3, 6

Dire si (Un) et (Vn) sont arithmétiques ou géométriques . Je trouve les 2 arithmétiques.

On pose Sn = Un + Vn
et Dn = Un - Vn

Exprimer Sn puis Dn en fonction de n.

C'est là que je ne comprends pas et j'ai beau chercher dans mes cours je ne trouve rien qui puisse m'orienter.

D'autant plus que la question suivante est :
exprimer Un et Vn en fonction de Sn et Dn.

Quelqu'un pourrait-il m'expliquer s'il vous plaît ? Merci d'avance à tous et bonne fin de journée.

par **ned aero** » 28 Mar 2010, 16:29

salut

Sn= 2n^(n-1) + 2n^(1-n), c'est exprimé en fonction de n

Dn= ....

...Sn= Un + Vn (1)
{
...DN= Un - Vn (2)

puis faire (1)-(2) puis (1)+(2)

par **axouten** » 28 Mar 2010, 21:20

Merci pour votre réponse mais je ne comprends toujours pas :

est-ce que le n-1 et le 1 - n sur la 1ère ligne sont en exposants ?

Comment on en arrive là ? Est-ce qu'il y a une propriété sur laquelle prendre exemple.

Je suis désolé de vous embêter mais j'aimerais comprendre.

Merci encore ned aero.

par **ned aero** » 28 Mar 2010, 21:30

oui c'est en exposant, je n'ai fais que reprendre l'énoncé...

il n'y a aucune formule ici, quand on dit par exemple:

Un = (1/2)^n, la suite (Un) est exprimée en fonction de n

pour le reste c'est comme un système

PS: les 2 suites ne sont ni arithmétiques ni géométriques

par **Hiphigenie** » 29 Mar 2010, 12:31

[font=Calibri]Bonjour,[/font]

[font=Calibri]Je pense que axouten définit

et

[/font]

[font=Calibri]Auquel cas : les premiers résultats pour la suite en U sont : 0, 2, 5, 10 et pour la suite en V sont 2, 2, 3, 6.[/font]

[font=Calibri]Ces deux suites ne sont ni arithmétiques, ni géométriques.[/font]

[font=Calibri]

qui est un suite géométrique dont le premier terme

et dont la raison est égale à 2.[/font]

[font=Calibri]

qui est une suite arithmétique dont le premier terme est

et dont la raison est égale à 2.[/font]

[font=Calibri]En appliquant les formules des suites, on pourra donner les valeurs de

et de

en fonction de n[/font]

par **ned aero** » 29 Mar 2010, 16:30

effectivement, j'avais compris que c'était (n-1) et (-n+1) qui étaient en exposant...bien entendu ça change tout..

Merci Hiphigenie pour axouten de lui avoir apporté un éclairage nouveau

par **axouten** » 31 Mar 2010, 16:30

Merci à vous deux,

Désolé de ne pas avoir répondu plus tôt mais j'avais des tournois (je fais du tennis).
Effectivement Hiphigénie, c'est la bonne écriture pour ma suite et après avoir lu votre message, j'ai repris mes calculs et j'ai trouvé mon erreur : j'ai un peu honte mais je le dis quand même, je comptais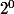

= 2 donc j'avais tout faux. Je sais je suis trop nul en maths.

Comme je l'avais dit à Ned Aero qui m'a aussi répondu gentiment, j'aimerais savoir comment vous faites pour arriver à trouver

et aussi savoir si les formules des suites sont : pour une suite géométrique

et une suite arithmétique

.
Si c'est ça, je nage complètement et je ne vois pas comment trouver la valeur de

en fonction de n.
Si vous n'avez pas le temps de m'expliquer, ce n'est pas grave, je sauterai cet exercice dans mon devoir parce que j'ai vraiment du mal à comprendre et ça :mur:
En tout cas merci encore à tous les deux et bonne soirée.

par **Hiphigenie** » 31 Mar 2010, 19:07

Il est marqué dans ton envoi de 15h52 :

On pose Sn = Un + Vn
et Dn = Un - Vn

Tu as, par définition dans ce même post, C et

.

Donc,

puisque les n se simplifient et les 1 également.

De même

puisque les

se simplifient.

Quant aux formules que tu as écrites, elles sont bien correctes si tu écris

pour la 1ère (le n est un exposant et non un indice).

par **axouten** » 31 Mar 2010, 19:18

Ah d'accord, merci beaucoup Hiphigenie.

C'est beaucoup plus clair pour moi. Je vais essayer de continuer tout seul merci encore et bonne soirée.

par **Mimi-S** » 31 Mar 2010, 19:51

Bonjour,
Est ce que quelqu'un pourrait m'aider sur 2 exo sur les suites svp ? C'est assez pressant. Merci

par **Hiphigenie** » 31 Mar 2010, 19:55

Mimi-S a écrit:Bonjour,
Est ce que quelqu'un pourrait m'aider sur 2 exo sur les suites svp ? C'est assez pressant. Merci

Bonsoir,

Tu devrais poser tes questions sur un nouveau post ... Il serait vu par tous les membres.

par **Mimi-S** » 31 Mar 2010, 20:12

Ah commen il fait faire ?

par **Mimi-S** » 31 Mar 2010, 20:15

Je vais sur " nouvelle discussion " ?

par **Hiphigenie** » 31 Mar 2010, 20:16

oui...c'est cela !

Suites

Suites

Suites numériques

Qui est en ligne