Suites (Spécialité)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Hitsugaya
- Membre Naturel
- Messages: 24
- Enregistré le: 08 Oct 2006, 10:08
-
 par Hitsugaya » 16 Oct 2006, 18:41
par Hitsugaya » 16 Oct 2006, 18:41
Bonsoir à tous !
Voila un petit exercice assez difficile que j'ai a faire en spé...
1) Le nombre 2^11 - 1 est il premier ?Non... car 2047=89*23
2) p et q sont deux entiers naturels, p  2 et q
2 et q  2.a) Justifier l'égalité
2.a) Justifier l'égalité p} + 2^{(q-1)p} = {1-2^{pq} \over 1-2^p})
Ici je sais qu'il faut se servir de la formule de sommation d'une suite géométrique.. mais comment l'utiliser, je bloque :/ Il faut prouver que c'est un suite géometrique deja.. et je n'arrive pas a trouver l'expression de la suite.
b) Quel est alors le reste de la division euclidienne de  par
par ) ?c) Montrer que
?c) Montrer que ) est divisible par
est divisible par ) et par
et par ) .3) n est un entier naturel. On veut maintenant montrer que si
.3) n est un entier naturel. On veut maintenant montrer que si ) est premier alors, n est premier.a) Enoncer la contraposée de cette proposition et la démontrer.
est premier alors, n est premier.a) Enoncer la contraposée de cette proposition et la démontrer.Si n n'est pas premier alors
)
n'est pas premier ? c'est ça ?
b) La réciproque de cette proposition est elle vraie ?Oula c'est la réciproque de la contraposée là ?
Voilà, comme vous pouvez le voir j'ai un peu de mal ^^ Donc si vous pourriez me donner un petit coup de pouce je vous en serait reconaissant...
Merci d'avance.
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 16 Oct 2006, 18:48
par Zebulon » 16 Oct 2006, 18:48
Bonsoir,
soit
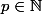
. Soit la suite (u_n) définie par
^n)
.
Calulez
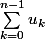
. Ca devrait vous aider...
-
Hitsugaya
- Membre Naturel
- Messages: 24
- Enregistré le: 08 Oct 2006, 10:08
-
 par Hitsugaya » 16 Oct 2006, 19:00
par Hitsugaya » 16 Oct 2006, 19:00
Bonsoir, ha d'accord merci je n'arrivais pas à trouver l'expression de la suite géométrique...
Le n ici c'est q alors ?
-
Hitsugaya
- Membre Naturel
- Messages: 24
- Enregistré le: 08 Oct 2006, 10:08
-
 par Hitsugaya » 16 Oct 2006, 19:23
par Hitsugaya » 16 Oct 2006, 19:23
Comment puis-je faire pour la question 1) b) ? Un petit indice ne serait pas de refus !
Merci
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 16 Oct 2006, 19:56
par Zebulon » 16 Oct 2006, 19:56
Hitsugaya a écrit:a) Justifier l'égalité p} + 2^{(q-1)p} = {1-2^{pq} \over 1-2^p})
Pour la question 1b, utilisez ce résultat.
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 16 Oct 2006, 19:57
par BancH » 16 Oct 2006, 19:57
Tu pourrais peut-être décomposer la question.
-Calculer le reste de la division euclidienne de
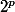
par
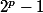
-Calculer le reste de la division euclidienne de
})
par
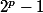
-Multiplier ces deux nombres.
-
Hitsugaya
- Membre Naturel
- Messages: 24
- Enregistré le: 08 Oct 2006, 10:08
-
 par Hitsugaya » 16 Oct 2006, 20:11
par Hitsugaya » 16 Oct 2006, 20:11
Je me doute bien qu'il faut utiliser ce résultat.. Mais... je n'y arrive pas... je suis resté 2 heures sur cet exercice a réflechir dessus... sans succès... Je pense que je vais laisser tomber. :/
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 17 Oct 2006, 17:30
par Zebulon » 17 Oct 2006, 17:30
Soit
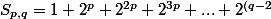p} + 2^{(q-1)p})
alors
S_{p,q})
quelle est donc la division euclidienne de

par
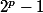
?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
