Suites - Relation de récurrence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 25 Avr 2013, 23:25
par upium666 » 25 Avr 2013, 23:25
Bonjour à tous et à toutes !
_{n \in \mathbb{N}} : \left\{\begin{matrix} u_0=1 \\ u_{n+1}=1+\frac{1}{u_n} \end{matrix}\right.)
Exprimer

en fonction de

...
(Aïe !)
Merci !

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 26 Avr 2013, 04:29
par capitaine nuggets » 26 Avr 2013, 04:29
Salut !
Calcule déjà les quatre-cinq premiers termes (peut-être que cela pourra aider à conjecturer quelque chose).
Pour ma part, je ne trouve vraiment pas quelque chose de très sympa pour l'instant ...
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 26 Avr 2013, 07:50
par Carpate » 26 Avr 2013, 07:50
capitaine nuggets a écrit:Salut !
Calcule déjà les quatre-cinq premiers termes (peut-être que cela pourra aider à conjecturer quelque chose).
Pour ma part, je ne trouve vraiment pas quelque chose de très sympa pour l'instant ...
On peut noter que

se développe sous la forme d'une fraction continue :
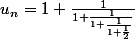
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Avr 2013, 09:41
par Kikoo <3 Bieber » 26 Avr 2013, 09:41
Je pense pas qu'il existe quelque chose pour cela !
La limite se calcule aisément, mais pour ce qui est de l'expression en fonction de n, niet...
Encore, si l'on avait une suite récurrente linéaire d'ordre 1, ou 2 !
-
Archytas
- Habitué(e)
- Messages: 1223
- Enregistré le: 19 Fév 2012, 13:29
-
 par Archytas » 26 Avr 2013, 10:13
par Archytas » 26 Avr 2013, 10:13
Salut, je ne sais pas si tu as vu les suites à récurrence linéraire (du type
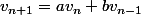
).
Je te propose la solution en rouge.
Si tu veux faire l'exo par toi même je te conseille de t'interesser aux suites à récurrence linéaires et à chercher une relation de récurence entre les termes de la suite
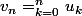
.
Une solution : On remarque que  et en posant
et en posant 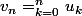 on obtient
on obtient  d'où
d'où  .
.il y a probablement plus simple, celà dit je pense que ça marche !
Edit: désolé Kikoo on s'est croisé, on avait la même idée apparement :ptdr: .

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 26 Avr 2013, 12:30
par leon1789 » 26 Avr 2013, 12:30
upium666 a écrit:Bonjour à tous et à toutes !
_{n \in \mathbb{N}} : \left\{\begin{matrix} u_0=1 \\ u_{n+1}=1+\frac{1}{u_n} \end{matrix}\right.)
Exprimer

en fonction de

...
u_n est le quotient de deux termes consécutifs de la suite de Fibonacci. C'est un autre moyen pour arriver aux formules (que je n'ai pas vérifiées) données par Archytas.
PS. au fait,
http://www.maths-forum.com/showthread.php?p=935573#post935573 ?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Avr 2013, 13:26
par Kikoo <3 Bieber » 26 Avr 2013, 13:26
Archytas a écrit:...
Une solution : On remarque que  et en posant
et en posant 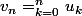 on obtient
on obtient  d'où
d'où  .
.il y a probablement plus simple, celà dit je pense que ça marche !
Edit: désolé Kikoo on s'est croisé, on avait la même idée apparement :ptdr: .
Jolie expression ! Je n'avais pas le courage de creuser davantage :p

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 26 Avr 2013, 16:04
par capitaine nuggets » 26 Avr 2013, 16:04
Archytas a écrit:Salut, je ne sais pas si tu as vu les suites à récurrence linéraire (du type
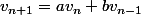
).
Je te propose la solution en rouge.
Si tu veux faire l'exo par toi même je te conseille de t'interesser aux suites à récurrence linéaires et à chercher une relation de récurence entre les termes de la suite
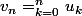
.
Une solution : On remarque que  et en posant
et en posant 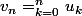 on obtient
on obtient  d'où
d'où  .
.il y a probablement plus simple, celà dit je pense que ça marche !
Edit: désolé Kikoo on s'est croisé, on avait la même idée apparement :ptdr: .
J'ai failli trouver la même chose, mais pas eu le courage de finir jusqu'au bout :triste:
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 26 Avr 2013, 21:43
par upium666 » 26 Avr 2013, 21:43
Archytas a écrit:Salut, je ne sais pas si tu as vu les suites à récurrence linéraire (du type
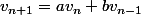
).
Je te propose la solution en rouge.
Si tu veux faire l'exo par toi même je te conseille de t'interesser aux suites à récurrence linéaires et à chercher une relation de récurence entre les termes de la suite
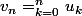
.
Une solution : On remarque que  et en posant
et en posant 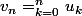 on obtient
on obtient  d'où
d'où  .
.il y a probablement plus simple, celà dit je pense que ça marche !
Edit: désolé Kikoo on s'est croisé, on avait la même idée apparement :ptdr: .
Que valent

et

?

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 26 Avr 2013, 23:00
par capitaine nuggets » 26 Avr 2013, 23:00
Salut !
upium666 a écrit:Que valent

et

?
Ce sont les solutions de l'équation
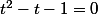
.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 27 Avr 2013, 06:30
par chan79 » 27 Avr 2013, 06:30
salut
on peut arriver à ça
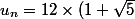^{n+1}-(1-\sqr{5})^{n+1}}{(1+\sqr{5})^{n}-(1-\sqr{5})^{n}})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
en fonction de
...
).
.
et en posant
on obtient
d'où
.
).
.
et en posant
on obtient
d'où
.
et
?