Suites réelles

[marc2015]

salut

j aime bien comprendre cette exercice

http://www.casimages.com/i/150811123719873881.png.html

1)soit un = n si n 10^2015
calculer la limite de la suite (un)

si n> 10^2015 limun=lim 1/n =0
mais pour
n 10^2015
calculer la limite de la suite (un)
si n> 10^2015 limun=lim -n/3 =-infini
mais pour
n<= 10^2015 lim un ?

si possible de me donner une réponse ( remarque la limite d une suite (un) ne dépend que des grandes valeurs de n ??)

merci

[bolza]

Bonsoir,

Ici quand on parle de la limite, c'est la limite quand n tend vers quoi ?
avec la réponse à cette question, et un peu de réflexion, tu devrais pouvoir t'en sortir

[marc2015]

salut bolza
merci j ai oublié d écrire n tend vers +infini
mais je n est pas compris des valeurs de n non grande est ce que la limite existe

pour l exercice comment repondre

merci

[bolza]

Et qu'est ce que cela signifie pour toi la limite de u_n quand n tend vers + infini ?

[capitaine nuggets]

Salut !

En général, quand on parle de limite d'une suite, il est sous-entendu qu'on parle de la limite en .

1) Ta première suite est définie pour les premiers termes par 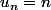et ensuite, à partir du rang , on a pour tout , .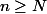

La nature d'une suite ne change pas si on retire un nombre fini de termes de cette suite, donc si on considère cette même suite mais définie à partir du rang (donc en enlevant les premiers termes de la suite ), on pose .
Ainsi les suites et ont même nature et même limite.

:+++:

[marc2015]

salut capitaine nuggets
merci pour vous explications
j aime bien que tu me donne plus d explications car je n est pas bien compris votre réponse
j aime bien savoir qu elle est la valeur de la limite de la suite
http://www.casimages.com/i/150811123719873881.png.html

la limite de la suites (un) ( n tend vers +infini) ( les deux questions sont indépendants
pour n 10^2015
calculer la limite de la suite (un)

si n> 10^2015 limun=lim 1/n =0 ( n tend vers +infini)
mais pour
n 10^2015
calculer la limite de la suite (un)
si n> 10^2015 limun=lim -n/3 =-infini
mais pour
n<= 10^2015 lim un ?

merci

[marc2015]

salut


j aime bien savoir qu elle est la valeur de la limite de la suite
la limite de la suites (un) ( n tend vers +infini) ( les deux questions sont indépendants
pour n 10^2015
calculer la limite de la suite (un)

si n> 10^2015 limun=lim 1/n =0 ( n tend vers +infini)
mais pour
n 10^2015
calculer la limite de la suite (un)
si n> 10^2015 limun=lim -n/3 =-infini
mais pour
n<= 10^2015 lim un ?

merci

[bolza]

Mmmmmmoui, et donc :

qu'est ce que cela signifie pour toi la limite de u_n quand n tend vers + infini ?

[marc2015]

bonsoir bolza

mon problème je n est pas compris
comment faire pour n<= 10^2015 pour les deux questions
donc la limite est égale a quoi

merci

[bolza]

bah si tu pose la question, c'est que tu n'a pas compris ce qu'est la limite d'une suite u_n quand n tend vers l'infini.
C'est pour ça que je te demande ce que ça signifie pour toi, je te demande pas une définition du cours,
mais juste que tu m'explique avec tes propres mots quel sens cela a pour toi.
ça m'aidera a t'expliquer ce qui ne va pas dans ta conception de limite.

(Si tu ne sais pas trop parce que c'est quelque chose de plutôt flou pour toi, tu as le droit le dire,
c'est pas grave, on est là pour t'expliquer ^^.)

[marc2015]

bonsoir bolza
oui je crois que je n est pas compris la notion de limite d une suite
donc pour moi la limite d une suite ne dépend que des grands valeurs de n
d ou dans notre cas pour les n tel que n<= 10^2015 ?

merci

[capitaine nuggets]

La limite d'une suite est un concept "local", c'est-à-dire qu'on s'intéresse au comportement de la suite de réels au voisinage de l'infini (lorsque devient infiniment grand).

Ta suite est définie pour tout entier dans par 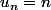et pour tout entier dans par .

Ce que j'affirme, c'est que la limite en de la suite ne dépend pas des premiers termes de la suite , donc au voisinage de l'infini les suites (u_n) et (1/n) sont équivalentes.

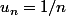Mais il y a encore plus simple lorsqu'on écrit , cela signifie qu'au bout d'un moment, dépasse puisqu'on veut le faire tendre vers l'infini. Donc lorsque ce dépasse le rang , donc .

:+++:

[bolza]

Non, la limite d'une suite est quelque chose qui quand elle existe est unique.
Elle ne dépend pas des valeurs de n.

En fait dire que n tend vers l'infini, c'est dire que n prend des valeurs de plus en plus grande.
Si la suite u_n a une limite, alors quand n va prendre des valeur de plus en plus grande, la suite
va être de plus en plus proche d'une valeur , que l'on va appeler l, et la limite de la suite est cette valeur l.

Prenons l'exemple de la suit v_n= 1/n comme tu l'as dit cette suite tend vers 0.
Si on regarde par exemple les différentes valeur de la suite pour des valeurs de n de plus en plus grande on a :

v_10 = 0,1
v_100=0,01
v_1000=0,001
...
v_1000000=0,000001

On voit que ce sont des valeurs qui sont de plus en plus proche de 0.

Maintenant si on modifie les 100 première valeur de la suite par exemple :

On a u_n = n si n < 100 et u_n = 1/n sinon.

Est-ce que cela change sont comportement "à l'infini" ?

Que se passe-t-il quand n tend vers l'infini ?
Si tu donne à la suite des valeurs de n de plus en plus grande, il y forcément un moment où n
va dépasser la valeur 100. Et qu'est-ce qui se passe quand n dépasse la valeur 100 ?
est bien la suite a exactement le même comportement que la suite v_n=1/n.

Autrement dit changer les premières valeurs d'une suite ne change pas son comportement à l'infini.
Parce que si tu change par exemple les k première valeur de la suite, alors quand n dépassera k,
la suite "retrouvera son comportement normal".

Bon, c'est peut-être pas très claire tous ça, mais j'espère que ça t'aidera un peu

Je te conseil de revoir ta définition de limite, et d'esssayé de bien la comprendre.

P.S. je ne me rappelle plus si au lycée on vous donne la définition avec des epsilon où si
c'est formulé autrement.

EDIT : Pardon capitaine, je n'ai pas vu ton poste, celui-ci est une réponse au poste d'avant

[zygomatique]

salut

quand on cherche la limite d'une suite donc la limite de la fonction c'est quand n tend vers +oo ....

donc on se fout des premiers termes ....

:ptdr:

[marc2015]

salut bolza

merci beaucoup oui c est très claire
oui en utilise la définition avec epsilon comment l utiliser ici

juste une autre question comment montrer que deux suites sont adjacentes ?

est ce qu il faut vérifier les trois conditions ou seulement deux conditions
1) un<=vn
2) un croissante et vn décroissante
3) lim(un-vn)=0

merci

[marc2015]

salut capitaine nuggets

merci beaucoup oui c est très claire

[capitaine nuggets]

salut bolza

merci beaucoup oui c est très claire
oui en utilise la définition avec epsilon comment l utiliser ici

juste une autre question comment montrer que deux suites sont adjacentes ?

est ce qu il faut vérifier les trois conditions ou seulement deux conditions
1) un<=vn
2) un croissante et vn décroissante
3) lim(un-vn)=0

merci

Salut, la définition ou une propriété que tu as vu te donne un certain nombre de condition : pourquoi hésiter à toutes les vérifier ? Peut-être crois-tu que seulement deux suffisent ? C'est possible, mais sauf preuve du contraire, tu dois garder toutes les conditions.

[bolza]

oui en utilise la définition avec epsilon comment l utiliser ici

dire que la suite converge vers une limite fini ,
c'est dire que :

Pour tout , il existe tel que pour tout , on a , il existe tel que pour tout , on a ), aussi petit soit-il,
on trouvera toujours un assez grand (i.e un rang à partir duquel) tout les termes de la suites sont proche de
(et donc si on choisis des intervalle de plus en plus petit, les termes de la suites seront de plus en plus proche de ).

Donc ça veut bien dire que la suite converge vers .

(Si j'explique tout ça c'est que beaucoup de personne apprenne la définition par cœur sans la comprendre,
et aussi parce que j'espère que cela vous apportera quelque éclaircissement sur la notion de limite.)

Donc à partir de là vous pouvez essayer de voir comment utiliser une telle définition.

P.S. : pour ce qui est des suites adjacentes, regarde la définition si dans la définition il y a les trois
alors c'est qu'il faut vérifier les trois. Tu peux essayer de trouver des contre exemples de suite
(non adjacente bien sûr) qui vérifie deux des trois points et pas le troisième, c'est un bon exercice.

[marc2015]

salut bolza
merci beaucoup c est très très claire
svp j aime bien que tu m explique la définition avec epsilon de la continuité d une fonction car je ne l est pas compris et comment l applique sur la fonction partie entière qui me pose un problème

svp est il possible de te contacter par message privé

merci

[bolza]

salut bolza
merci beaucoup c est très très claire
svp j aime bien que tu m explique la définition avec epsilon de la continuité d une fonction
car je ne l est pas compris et comment l applique sur la fonction partie entière qui me pose un problème

svp est il possible de te contacter par message privé

merci

Bonsoir,

Pour les fonction continue, c'est à peu près le même principe,
l'idée c'est si x varie très peu alors f(x) varie aussi très peu,
car si f(x) varie beaucoup quand x varie très peu, ça veut dire qu'on a un "saut" (une discontinuité).
Formuler autrement on peut dire que si "y est proche de x" alors "f(y) est proche de f(x)",
et si vous reprenez la notion de proche que j'ai expliqué plus haut,
vous retombez normalement sur la définition avec epsilon.
Mais le mieux pour comprendre ce genre de chose c'est de faire des dessins .

Mais là on s'égare du sujet, vous savez si il y a des définitions de cours que vous ne comprenez pas,
posez des questions à votre professeur de math, il est là pour ça
(vous me direz, on est sur le forum de soutiens scolaire en math qui est fait pour ça aussi ^^.
On peut communiquer par mp si vous voulez, mais le mieux je pense c'est d'ouvrir
un nouveau sujet pour chaque nouvelle question

P.S. : si vous avez des problèmes pour appliquer la définition de fonction continue à la partie entière,
c'est normal car ce n'est pas une fonction continue !!