Suites reelles

[blopishere]

Bonjour!

J'ai un devoir à faire sur le triangle de Sierpinski, dont voici l'enoncé :

On dispose au départ d'un triangle équilatéral de côté 3cm dont l'intérieur est noir. A la première étape, on construit le triangle des milieux que l'on colorie en blanc. A la deuxième étape, on répète l'opération pour chacun des trois triangles noirs de l'étape 1. Et ainsi de suite indéfiniment.

On s'interesse aux triangles blancs T(n) construits lors de la n-ième étape. Pour n>=1, on désigne par p( n) le périmètre et par a(n) l'aire d'un triangle Tn(n)

1. calculer u1 (=1), p1 (=9/2) , et a1 (=9 racine de 3/16)
2 Indiquer comment u2 , p2 , et a2 s'obtiennent simplement à partir de u1 , p1 et a1
u2 =u1 +3
p2 =(1/2)*p1
a2 =(1/8)*a1 (là, je ne suis pas sûre, est-ce (1/8) ou (1/4)?)

Cela reste vrai à l'étape n+1 pour p et a, mais pas pour u, et il faut ensuite déduire la nature des suites (les 2 dernières sont donc géométriques, c'est juste?), mais comment faire pour la suite u?

Il me semble que u(n+1)=3u(n)+1, mais je ne vois pas trop comment le prouver, j'ai trouvé cette suite en faisant les calculs successifs des triangles...

Merci beaucoup!

[Daragon geoffrey]

slt
déjà trace les rectangles successifs et vérifie ds les 2 ou 3 premiers cas que les triangles obtenus à chaque nouvelle étape sont isométriques ! angles égaux et même longueur des côtés ! ça va assez vite.
ensuite cherche une façon de définir de façon EXPLICITE une suite te donnant la longueur du n-iècôté : je trouve Un=3/2^n, sachant que la hauteur est obtenue par l'application de la trigonométrie ds les triangles équilatéraux : h=a*sin(pi/3)=a*racine(3)/2, or a=longueur du côté donc a(n)=3/2^n et A=b*h/2 (base fois hauteur * 0.5=aire d'un triangle) donc A(n)=aire du n-ième triangle=9*racine(3)/2^(2n+2)
de plus P=périmètre=3a=3*3/2^n=9/2^n
voilà je pense que c bon, tu nas plus qu'à étudier ces deux suites : dérivées pour sens de variation, ou th. de rangement des nombres ... bref tu as le choix, et convergence !

[Daragon geoffrey]

dsl g fait une erreur d'inattention o début du précédent message, ce n'est pas "trace les rectangles..." mais les "triangles..."

[Sasuke_Uchina]

Bonjour,

Il n'y a pas de définition pour . Si c'est le nombre total des triangles blancs , c'est juste la somme d'une suite géométrique de raison 3 , avec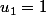

le coté d'un triangle devient la moitié de celui du trianle précédent , donc




donc si on connait et , on obtient l'expression explicite. ( et 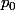n'existent pas bien sur )

[blablabla00110011]

Bonjour, je ne comprend pas d'où il faut partir pour arriver a démontrer Un=3/2^n et A(n)=9*racine(3)/2^(2n+2)
merci

[Ben314]

Salut,
Si je comprend bien l'énoncé on a :
périmètre de chacun des triangles blancs créés lors de l'étape n (ils sont tous la même taille)
aire de chacun des triangles blancs créés lors de l'étape n.
= nombre de triangles blanc créés lors de l'étape ( 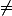nombre total de triangles blancs que l'on a l'issue de l'étape n)
A la base, c'est pas trop malin de compter directement le nombre total de triangle blancs que l'on a vu qu'ils ne sont pas tous de la même taille donc qu'on ne saura pas comment en déduire l'aire de la surface coloriée en blanc alors que tout les triangles créés lors de la même étape sont de même taille.

Ensuite, si on veut tout bien rédiger comme il faut, il faut commencer par quelques constatations simples :
- Partant d'un triangle équilatéral noir (de taille quelconque), si on colorie en blanc le "triangle des milieu" de ce triangle, la partie restée noire est constituée de 3 triangles équilatéraux de même taille que le triangle blanc créé.
- Cela signifie que, si à l'étape n on a créé un certain nombre de nouveaux triangles blancs alors il y a sur le dessin 3 fois plus de triangles noirs. Donc à l'étape suivante, on créera 3 fois plus de nouveaux triangles blancs qu'à cette étape là :
- Cela signifie aussi que, à l'issue d'une étape donnée, tout les triangles noirs sont de même taille qui est la même que celle des triangles blancs que l'on vient juste de créer (par contre il y aura aussi des triangles blancs plus gros provenant des étapes précédentes). Donc la taille des triangles blancs que l'on va créer à l'étape suivante sera la taille des "triangles des milieu" des triangles blancs que l'on vient juste de créer.
- Le "théorème des milieux" nous dit que les longueurs des cotés du "triangle des milieu" d'un triangle donné sont égales à la moitié des longueurs des cotés du triangle de départ. Donc le "triangle des milieux" a un périmètre égal à la moitié de celui de départ ce qui, vu le point précédent, montre que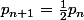
- Enfin, on a dit dans le premier point que, lorsque l'on colorie en blanc le triangle du milieu d'un triangle noir, cela forme 4 nouveaux triangles (3 noirs et 1 blanc) de même taille (donc de même aire). L'aire des nouveaux triangles créés est donc égale au quart de l'aire du triangle de départ. Donc .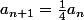

Bilan : les trois suites sont des suites géométriques donc pour chacune d'elle, il suffit de connaitre la valeur du premier terme pour en déduire la valeur du n-ième.

[blablabla00110011]

salut
pour chaque suite u0=0 non? puisque a l'étape 0 il n'y a pas de triangle blanc

[Ben314]

= nombre de triangles blanc créés lors de l'étape ( nombre total de triangles blancs que l'on a l'issue de l'étape n)

De plus, personnellement moi même tout seul, quand je répète un certain nombre de fois une tâche, ben la tache du début que c'est que je commence avec par la faire... ben c'est pas la "zéroième".

Par exemple là, je sais pas trop te dire combien il y a de "triangles blancs créés lors de la zéroième étape".

[blablabla00110011]

merci beaucoup

[blablabla00110011]

donc ya pas de Uo ?

[Ben314]

On dispose au départ d'un triangle équilatéral de côté 3cm dont l'intérieur est noir. A la première étape, on construit le triangle des milieux que l'on colorie en blanc. A la deuxième étape, on répète l'opération pour chacun des trois triangles noirs de l'étape 1. Et ainsi de suite indéfiniment.

Quand tu construit un modèle en Lego et que sur la doc. tu tombe sur la page marqué première étape, tu cherche la page précédente ?

[blablabla00110011]

d'accord merci