Bien que je ne sois pas sûr de t'aider en te faisant le devoir (je pense que tu ne devrais pas poster un devoir entier, mais plutôt une ou deux questions sur lesquelles tu bloques); le voici: Des éléments cylindriques ont un diamètre d= 40 cm et une longueur l=25 dm
1) calculer en m², le volume occupe par un élément (a 10-² près par excès)
1) Le volume ne s'exprime jamais en mètres carrés (réservés aux surfaces), mais en mètres cubes. Le volume d'un cylindre est donné par la relation:
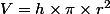
où r est le rayon de la base, et h la hauteur du cylindre
Cela donne donc:
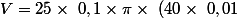^2=0,32m^3)
2) pour le rangement de ces éléments, on les dispose en ranges superposes comme lindique la figure.
a- quelle relation existe-t-il entre le nombre délément dispose au sol et le nombre total de rangées que lon peut constituer ? Exprimer ce résultat a laide dune phrase complète.
2) a) On remarque qu'on peut constituer autant de rangées qu'il y a d'éléments disposés au sol.
b- Si N est le nombre délément dune range, quel est le nombre déléments de la ranger immédiatement supérieure ?
b) Soit N le nombre d'élèment d'une rangée tel que N>1. On peut ranger 1 élèment de moins à la rangée supérieure, soit N-1 élèments.
c- La série numérique formée par le nombre délément sur les ranges successive en partant du sol est elle arithmétique ou géométrique ?quel est sa raison ?
c) D'après la question précédente, on peut affirmer que la suite numérique formée par le nombre d'éléments sur les rangées successives en partant du sol est une suite arithmétique de raison -1 et de premier terme u1=le nombre d'éléments au sol.
d- Il semble que le nombre total déléments A que lon puisse ranger de cette façon en posant N élément au sol soit donne par relation : A=N (N+1) divise par 2.Cela est t-il vérifier pour n=5 ? justifier votre réponse
d) Pour N=5, on pourra ranger A=5+4+3+2+1=15 éléments cylindriques.
Calculons

:
}{2}=\frac{30}{2}=15)
Donc pour N=5,
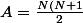
et la relation est verifiee.
Le tablier dun pont est retenu par des groupes de 25 cables.ces câbles sont numérotes de 1 a 25 du plus court au plus long comme lindique le shema
Dans le tableau suivant figure les longueurs ln des 6 premiers câbles
1-calculer L2-L1 , L3-L2 et l4- l5
On pose:
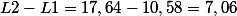
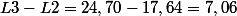
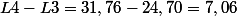
2-les longueurs Ln des câbles forment elles une suite arithmétique ou géométrique ?justifier la réponse
3-donner le premier terme de cette suite ainsi que sa raison.
2 et 3) D'après la question 1, on remarque que: L2-L1=L3-L2=L4-L3=7,06 et L1=10,58
Il s'agit donc d'une suite arithmétique (vn) de premier terme v1=10,58 et de raison 7,06
4-calculer la longueur du 2 eme câble
4) D'après la question précédente, (vn) est une suite arithmétique de premier terme v1=10,58 et de raison 7,06; la forme explicite de (vn) est donc:
Pour tout entier naturel n >= 1,
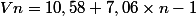)
D'après cette relation,
=10,58+7,06\times\(2-1)=17,64)
On remarque que cette valeur est conforme à celle du tableau.
5-un des câbles a une longueur de 151.78m ; quel est le numéro de ce câble
5) Soit n un entier naturel tel que n >= 1
On veut résoudre:
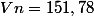
=151,78)
=141,2)
=20)
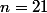
Donc le cable qui a une longueur de 151,78m est le cable numéro 21.
- Bonne continuation.



