Suites et ordres 2

[doudia]

Bonsoir, si( Un) est une suite numerique tel que quelque soit n appartenant à IN Un>a avec Un convergente est ce que je peux dire que quand n tend vers plus l'infini lim Un >= a

[mathelot]

la réponse est oui. Si l'on veut démontrer, on étudie la contraposée.

[doudia]

Ahhhh donc je dois juste demontrer que lim Un<a implique que Un<a cela semble évident mais je ne sais pas comment faire

[Tuvasbien]

Attention, lorsqu'on écrit lim u_n = a on sous entend "(u_n) admet une limite et celle ci vaut a", la négation est alors "(u_n) n'admet pas de limite ou (u_n) ne tend pas vers a", le mieux est de revenir à la définition avec des epsilons.

[mathelot]

on suppose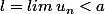
on prend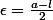
pour n suffisamment grand:

[pascal16]

l : la limite
on peut partir de "l-a".
on pose epsilon = (l-a)/2

le fait que proche de la limite tous les terme de la suite soient proches de l à epsilon prêt permet de conclure

[doudia]

D'accord c'est ce que je voulais comprendre merciii

[mathelot]

Attention, lorsqu'on écrit lim u_n = a on sous entend "(u_n) admet une limite et celle ci vaut a", la négation est alors "(u_n) n'admet pas de limite ou (u_n) ne tend pas vers a", le mieux est de revenir à la définition avec des epsilons.

P,Q,R étant des prédicats,
On a une implication de la forme


que l'on transforme en
Soit R.

la contraposée est :
Soit R.