Suites numériques
2 messages
- Page 1 sur 1
Suites numériques
par Sam74 » 27 Fév 2021, 12:21
H
Modifié en dernier par Sam74 le 27 Fév 2021, 13:46, modifié 1 fois.
Re: Suites numériques
par hdci » 27 Fév 2021, 13:03
Bonjour,
On veut que)
soit géométrique. Si q est sa raison, on veut donc que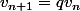 
pour tout entier n
Si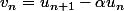
, alors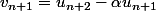 
On remplace alors
et 
dans la relation géométrique :
)
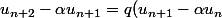Puis on remplace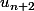
par sa relation de récurrence
)
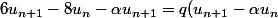Ce qui fait (dans une équation, un bon réflexe est de comparer à zéro)
u_{n+1}+(q\alpha-8)u_n=0)
On veut que ce soit vrai pour tout n, donc pour toutes les valeurs de
et 
. Une condition suffisante est que les deux coefficients multipliant les termes soient nuls, soit
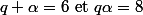
Je vous laisse terminer la résolution de ce système de deux équations à deux inconnues (on exprime q en fonction de alpha dans la première ligne, et on remplace q dans la seconde ligne par ce qu'on vient de trouver, cela donne une équation du second degré en alpha)
On veut que
Si
On remplace alors
Puis on remplace
Ce qui fait (dans une équation, un bon réflexe est de comparer à zéro)
On veut que ce soit vrai pour tout n, donc pour toutes les valeurs de
Je vous laisse terminer la résolution de ce système de deux équations à deux inconnues (on exprime q en fonction de alpha dans la première ligne, et on remplace q dans la seconde ligne par ce qu'on vient de trouver, cela donne une équation du second degré en alpha)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :