Suites numériques : exprimer Un+1 en fonction de Un

[alex778]

Bonsoir, je rencontre des difficultés à résoudre cet exercice :
Un=2n²-5n-7
On doit ensuite calculer Un+1 et Un-1 en fonction de N :
Un-1=2(n-1)²-5(n-1)-7
Un+1=2n²-n-10
On doit ensuite définir Un+1 en fonction de Un mais je en vois pas comment faire.

Pourriez-vous m'aider ?

Merci d'avance !

[zygomatique]

salut

u_{n + 1} - u_n = .... ?

[alex778]

Un+1-Un=2n²-5n-7-(2n²-n-10)
=-4n+3
Ca ferait donc Un+1=Un-4n+3 ?

[Ben314]

C'est une réponse... possible...
Mais l'énoncé est légèrement ambigüe : doit on exprimer uniquement en fonction de (et pas de ) ou bien en fonction 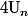de et de ?

Ta réponse est correcte dans le second cas, mais ce second cas me semble franchement inintéressant vu qu'on pourrait répondre des tas de chose, en particulier on pourrait répondre (bêtement) que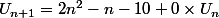

Donc, à mon avis, il faut s'en tenir à la première formulation, c'est a dire uniquement en fonction de Un.
Sauf que ce n'est pas évident du tout dans ce cas là.
Le seul truc qui me vient à l'esprit, c'est de calculer n en fonction de Un (c'est une équation du second degrés) et d'injecter le résultat dans la formule donnant U(n+1) en fonction de n.

[alex778]

C'est une réponse... possible...
Mais l'énoncé est légèrement ambigüe : doit on exprimer uniquement en fonction de (et pas de ) ou bien en fonction de et de ?

Ta réponse est correcte dans le second cas, mais ce second cas me semble franchement inintéressant vu qu'on pourrait répondre des tas de chose, en particulier on pourrait répondre (bêtement) que

Donc, à mon avis, il faut s'en tenir à la première formulation, c'est a dire uniquement en fonction de Un.
Sauf que ce n'est pas évident du tout dans ce cas là.
Le seul truc qui me vient à l'esprit, c'est de calculer n en fonction de Un (c'est une équation du second degrés) et d'injecter le résultat dans la formule donnant U(n+1) en fonction de n.

Le sujet dit simplement : "Exprimer Un+1 en fonction de Un."
C'est censé être un exercice de base sur les suites donc il n'est pas censé être trop complexe, surtout qu'on a peu avancer dans le cours. Il n'y as pas d'autres solutions d'après vous ?

[Ben314]

Est-ce que la question n'est pas plutôt "Exprimer en fonction de et de ? (là, il y a des réponses simples)

Sinon, est-ce que tu as d'autre questions ensuite (pour voir si il y a une logique derrière tout ça) ?

[alex778]

La question d’après est " A partir de quel rang Un est elle positive ?". Ca je l'ai fais sans soucis. La question précédente n'inclue pas Un-1.

[Ben314]

Donc je vois rien d'autre à faire que d'y aller super bourrin et de retrouver n connaissant Un...
On a qui est une équation du second degré en .
Le discriminant est et il est forcément positif vu qu'on sait qu'il existe un vérifiant la relation.
Donc et c'est pas très clair de savoir si c'est un + ou un -.
Tout ce qu'on peut dire, c'est que, vu que doit être positif, si (ce qui est rapidement le cas) on est sûr que
Et on en déduit que :





Mais ça me parrait louche que ce soit ça qui soit attendu...

[mathelot]

bonjour,

[Ben314]

Oui mais, si tu lit TOUT les post précédents, tu y trouvera :

Est-ce que la question n'est pas plutôt "Exprimer en fonction de et de ? (là, il y a des réponses simples)

puis

...La question précédente n'inclue pas Un-1.

[mathelot]

je rendrais ça comme résultat

[Ben314]

De toute façon à mon avis, il y a un bug. dans l'énoncé vu le niveau des autres questions.

Sinon concernant la récurrence "double", il y a de nouveau une infinité de solutions, par exemple on pourrait aussi écrire que, comme , on a