Bonsoir, j'ai un exercice sur les suites mais je ne sais pas par quoi commencer, je n'ai aucunes pistes.. Est ce que quelqu'un pourrait m'expliquer ? Le sujet et en pièce joint ici : http://zupimages.net/up/16/40/rb1j.jpg
Merci d'avance
Suites numérique Terminale S
7 messages
- Page 1 sur 1
Re: Suites numérique Terminale S
Bonsoir,
Cette suite est très connue, c'est la suite de Syracuse (ou de Collatz). Regardes ce que ça donne quand tu poses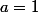 : tu devrais avoir une séquence qui se répète.
: tu devrais avoir une séquence qui se répète.
Eh bien la seule chose à savoir, c'est que tu retomberas toujours sur cette séquence à un moment ou un autre. Essaies de prendre d'autres valeurs de pour voir ce que ça donne.
pour voir ce que ça donne.
Néanmoins ce résultat est une simple conjecture, on n'a jamais réussi à démontrer que l'on retombait tout le temps sur cette séquence, c'est juste que ça a marché pour tous les exemples testés jusqu'à aujourd'hui.
Cette suite est très connue, c'est la suite de Syracuse (ou de Collatz). Regardes ce que ça donne quand tu poses
Eh bien la seule chose à savoir, c'est que tu retomberas toujours sur cette séquence à un moment ou un autre. Essaies de prendre d'autres valeurs de
Néanmoins ce résultat est une simple conjecture, on n'a jamais réussi à démontrer que l'on retombait tout le temps sur cette séquence, c'est juste que ça a marché pour tous les exemples testés jusqu'à aujourd'hui.
Re: Suites numérique Terminale S
bjr
voir ce lien pour comprendre
http://villemin.gerard.free.fr/Wwwgvmm/ ... racuse.htm
et ce lien
http://calculis.net/syracuse
voir ce lien pour comprendre
http://villemin.gerard.free.fr/Wwwgvmm/ ... racuse.htm
et ce lien
http://calculis.net/syracuse
Re: Suites numérique Terminale S
samoufar a écrit:Bonsoir,
Cette suite est très connue, c'est la suite de Syracuse (ou de Collatz). Regardes ce que ça donne quand tu poses: tu devrais avoir une séquence qui se répète.
Eh bien la seule chose à savoir, c'est que tu retomberas toujours sur cette séquence à un moment ou un autre. Essaies de prendre d'autres valeurs depour voir ce que ça donne.
Néanmoins ce résultat est une simple conjecture, on n'a jamais réussi à démontrer que l'on retombait tout le temps sur cette séquence, c'est juste que ça a marché pour tous les exemples testés jusqu'à aujourd'hui.
Bonsoir, donc la particularité de cette suite repose juste sur le fait que l'on retombe toujours sur la meme séquence ?
Re: Suites numérique Terminale S
Je pense oui.
Tu peux tenter de le prouver par toi même, mais personne jusqu'à maintenant n'a su le faire....
Tu peux tenter de le prouver par toi même, mais personne jusqu'à maintenant n'a su le faire....
Re: Suites numérique Terminale S
nodgim a écrit:Je pense oui.
Tu peux tenter de le prouver par toi même, mais personne jusqu'à maintenant n'a su le faire....
D'accord merci
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
