Suites niveau Term S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
chouxette
- Messages: 6
- Enregistré le: 07 Sep 2016, 20:31
-
 par chouxette » 09 Sep 2016, 12:43
par chouxette » 09 Sep 2016, 12:43
Bonjour,
Voici un exercice que je dois faire pour demain et je bloque, pourtant il a l'air assez simple ^^

- L'exercice :
- mathssss.jpg (60.93 Kio) Vu 515 fois
J'en suis là :
1) An = Un+1 - Un
An = -2Un + 3 Un-1 - Un
An = - 3Un + 3 Un-1
An = 3 (-Un + Un-1)
Je suis partie là dessus ... c'est bon ou pas ? ^^ Et je me retrouve bloquée là car je ne sais pas quoi faire ensuite ...
Merci d'avance, et désolée je ne sais pas comment faire pour écrire avec des indices

-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 09 Sep 2016, 13:07
par Razes » 09 Sep 2016, 13:07
chouxette a écrit:J'en suis là :
1) An = Un+1 - Un
An = -2Un + 3 Un-1 - Un
An = - 3Un + 3 Un-1
An = 3 (-Un + Un-1)
Près de la ligne d'arrivée.

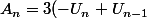= -3 (U_n - U_{n-1})=-3A_{n-1})
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 09 Sep 2016, 13:19
par Carpate » 09 Sep 2016, 13:19
1) An = Un+1 - Un --> An= 1 !
Ecris : A(n)=U(n+1)-U(n) ou utilise le langage LaTeX :
A_n=U_{n+1}-U_n qui, inséré entre balises rex (bouton tex au-dessus), donne
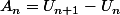
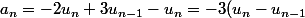=-3a_{n-1})
-
chouxette
- Messages: 6
- Enregistré le: 07 Sep 2016, 20:31
-
 par chouxette » 09 Sep 2016, 19:17
par chouxette » 09 Sep 2016, 19:17
D'accord merci beaucoup, en effet c'est super simple mais j'ai du mal à faire le lien

Donc la raison est -3 c'est ça ? Et pour le premier terme je dois remplacer par les valeurs

dans la première suite

pour ensuite trouver la valeur
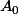
?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 09 Sep 2016, 20:02
par Carpate » 09 Sep 2016, 20:02
Ben oui :
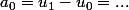
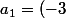 a_0)
a_n=(-3")^n a_0
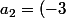^2a_0)
...
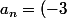^n a_0=...)
-
chouxette
- Messages: 6
- Enregistré le: 07 Sep 2016, 20:31
-
 par chouxette » 09 Sep 2016, 20:45
par chouxette » 09 Sep 2016, 20:45
Voici mon DM en entier, c'est juste ?

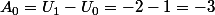
Donc le premier terme est -3.
B)
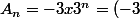^(n+1))
2)
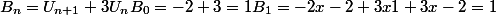
Donc
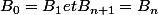
3) On a donc
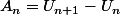
et
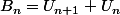
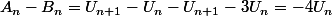
donc
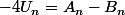
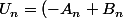/4 =[ - (-3)^(n+1) + 1 ]/4)
C'est bon comme ça ?
Merci d'avance !

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 09 Sep 2016, 20:55
par anthony_unac » 09 Sep 2016, 20:55
chouxette a écrit: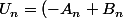/4 =[ - (-3)^(n+1) + 1 ]/4)
C'est bon comme ça ?
Merci d'avance !
Bonsoir,
Vous pouvez facilement contrôler par vous même votre relation finale en essayant les premières valeurs

puis

par exemple

-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 09 Sep 2016, 20:59
par Razes » 09 Sep 2016, 20:59
Pour le signe de la multiplication utilise le point "." ou \times qui donne

-
chouxette
- Messages: 6
- Enregistré le: 07 Sep 2016, 20:31
-
 par chouxette » 09 Sep 2016, 21:30
par chouxette » 09 Sep 2016, 21:30
D'accord merci !
Mais je ne suis pas sûre de mon raisonnement pour la question 2 ... remplacer par les valeurs suffit ? Ce n'est pas plus compliqué que ça ?
-
chouxette
- Messages: 6
- Enregistré le: 07 Sep 2016, 20:31
-
 par chouxette » 09 Sep 2016, 21:36
par chouxette » 09 Sep 2016, 21:36
Après reflexion je viens de voir que la réponse à la question 2 est sans doute cela
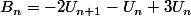
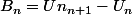
Or
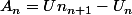
donc
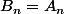
Qu'en pensez vous ?
Modifié en dernier par
chouxette le 09 Sep 2016, 21:37, modifié 1 fois.

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 09 Sep 2016, 21:37
par anthony_unac » 09 Sep 2016, 21:37
Ce n'est qu'un contrôle comme la preuve par neuf pour vérifier le résultat d'une multiplication.
Vous pouvez pousser le bouchon jusqu'à n=3 si vous êtes sceptique.
Vous pouvez aussi redémontrer votre relation finale par récurrence si vous êtes courageux

-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 09 Sep 2016, 22:07
par Razes » 09 Sep 2016, 22:07
chouxette a écrit:Voici mon DM en entier, c'est juste ?

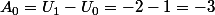
Donc le premier terme est -3.
B)
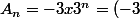^(n+1))
2)
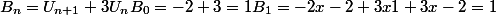
Donc
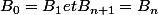
Jusqu'à là c'est bon.
3)Tu as trouvé:
 Calcul la somme
Calcul la somme des deux équations. Que trouves tu?
Remplace
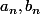
par leurs valeurs
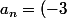^{n+1}\\b_n=1)
Que trouves tu?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités

