Suites et intégrales
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Sulaheia
 par Sulaheia » 18 Sep 2017, 10:36
par Sulaheia » 18 Sep 2017, 10:36
Bonjour bonjour,
J'ai l'exercice suivant :Soit
)
définie pour

par :

1 - Démontrer que pour tout
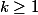
:

2 - En déduire que

3 - En déduire le comportement asymptotique de
) Voici ce que j'en ai fait, avec mes questions en gras :
Voici ce que j'en ai fait, avec mes questions en gras :1/ : on veut montrer que
 - ln(k) \leq \dfrac{1}{k})
Ok, mais j'ai utilisé le fait que x>ln(x) -
j'ai le droit d'affirmer ça en TS ?2/ - Ok, c'est la somme des petites intégrales (je me comprends

).
3/
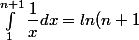 - ln(1) = ln(n+1))
, ça tend vers l'infini, donc la suite aussi par comparaison.
C'est tout ? Le "comportement asymptotique", c'est juste la limite ? Merci !
-
cailloux1
- Membre Naturel
- Messages: 40
- Enregistré le: 18 Nov 2013, 21:44
-
 par cailloux1 » 18 Sep 2017, 12:05
par cailloux1 » 18 Sep 2017, 12:05
Bonjour,
1) Pour tout
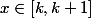
,

et on intègre sur
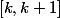
3)
)
or
=+\infty)
Avec les théorèmes de comparaison:
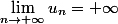
et oui: on a le "comportement asymptotique" de
)

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 18 Sep 2017, 13:02
par Lostounet » 18 Sep 2017, 13:02
Sulaheia a écrit:3/
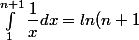 - ln(1) = ln(n+1))
, ça tend vers l'infini, donc la suite aussi par comparaison.
C'est tout ? Le "comportement asymptotique", c'est juste la limite ? Merci !
Salut,
En fait le comportement asymptotique désigne non seulement la limite mais aussi "comme quoi se comporte la quantité".
La morale de cet exercice est le fait "surprenant" suivant. Informellement:
S = 1+1/2+1/4+..... vaut + infini. Malgré le fait d'ajouter des quantités de plus en plus petites! C'est étonnant non?
Et l'exercice te propose en plus de montrer que cette somme tend vers +infini au même rythme que ln(n) (donc lentement mais..surement).
La technique utilisée s'appelle "comparaison série intégrale" ou monotonie intégrale. Il faut absolument faire une figure si tu ne vois pas la question 1) c'est assez intuitif.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Sulaheia
 par Sulaheia » 19 Sep 2017, 06:47
par Sulaheia » 19 Sep 2017, 06:47
@lostounet - On peut parler de courbe asymptote en terminale ? Ou on dit informellement que ça se rapproche de telle ou telle fonction ?
Pour la question 1, @cailloux1 et @lostounet : mais carrément ! J'ai bien fait de vous poser la question, merci beaucoup !!! En fait j'avais oublié ce que c'était une intégrale

.
(c'est marrant, hier j'ai lu vos réponses et je voyais pas du tout de quoi vous vouliez me parler - j'ai bien fait d'attendre un peu pour répondre)
Mais quand même (même si j'en ai pas besoin ici) : j'ai le droit d'affirmer sans le démontrer que x>ln(x) ?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 19 Sep 2017, 07:13
par Lostounet » 19 Sep 2017, 07:13
Hey,
Il suffit de poser pour x>0 f(x)=x-ln(x) et l'étudier !
Généralement l'inégalité de concavité est ln(x)<=x-1
Moi ça me gêne pas de parler d'asymptote en terminale (voire de branche parabolique). mais bon..
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
