Suites géométriques et arithmétiques
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
par maths0 » 20 Avr 2012, 00:33
Ce n'est pas la bonne méthode
et
.
Normalement tu devrais faire:
 + 3}}{2} + \frac{{3 \times {2^{n + 1}} + 4\left( {n + 1} \right) - 3}}{2}\\<br />{w_{n + 1}} = \frac{{3 \times {2^n} \times 2 - 4\left( {n + 1} \right) + 3}}{2} + \frac{{3 \times {2^n} \times 2 + 4\left( {n + 1} \right) - 3}}{2}<br />\end{array})
Ou alors dans ce que tu as fait, il faut bien marquer par identification ... est la raison .. est le premier terme. J'ai pas vérifier si c'est juste. Je fais le calcul et je poste.
C'est un peu le bordel, d'où tes blocages.
Si tu sais que (wn) est géométrique alors elle s'écrit .... wn= ...
Si tu sais que (tn) est arithmétique alors elle s'écrit .... tn= ...
Donc 1/2(wn+tn)= ...
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
par maths0 » 20 Avr 2012, 00:41
 + 3}}{2} + \frac{{3 \times {2^{n + 1}} + 4\left( {n + 1} \right) - 3}}{2}\\ {w_{n + 1}} = \frac{{3 \times {2^n} \times 2 - 4\left( {n + 1} \right) + 3}}{2} + \frac{{3 \times {2^n} \times 2 + 4\left( {n + 1} \right) - 3}}{2}\\ {w_{n + 1}} = \frac{{6 \times {2^n} - 4n - 4 + 3 + 6 \times {2^n} + 4n + 4 - 3}}{2}\\ {w_{n + 1}} = \frac{{12 \times {2^n}}}{2}\\ {w_{n + 1}} = 6 \times {2^n} \end{array})
Comment trouves-tu la même chose avec wn ?
Cela voudrait dire que:
alors que c'est en vrai
Tu as vérifié le calcul de wn que tu as fait ? ?
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
par M@thIsTheBest » 20 Avr 2012, 00:44
Je veux savoir d'abord votre niveau scolaire, pour que je puisse écrire une démonstration adéquate.
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
par maths0 » 20 Avr 2012, 00:45
C'est 1ere S M@thIsTheBest.
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
par Xeniuss » 20 Avr 2012, 00:45
maths0 a écrit:Ce n'est pas la bonne méthode
et
.
Normalement tu devrais faire:
 + 3}}{2} + \frac{{3 \times {2^{n + 1}} + 4\left( {n + 1} \right) - 3}}{2}\\ {w_{n + 1}} = \frac{{3 \times 2 \times 2 - 4\left( {n + 1} \right) + 3}}{2} + \frac{{3 \times {2^n} \times 2 + 4\left( {n + 1} \right) - 3}}{2} \end{array})
Ou alors dans ce que tu as fait, il faut bien marquer par identification ... est la raison .. est le premier terme. J'ai pas vérifier si c'est juste. Je fais le calcul et je poste.
C'est un peu le bordel, d'où tes blocages.
Si tu sais que (wn) est géométrique alors elle s'écrit .... wn= ...
Si tu sais que (tn) est arithmétique alors elle s'écrit .... tn= ...
Donc 1/2(wn+tn)= ...
Ha d'accord la je comprend beaucoup mieux, mais je ne comprend pas d'où sort le x2 a la 2eme ligne du calcul
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
par Xeniuss » 20 Avr 2012, 00:46
M@thIsTheBest a écrit:Je veux savoir d'abord votre niveau scolaire, pour que je puisse écrire une démonstration adéquate.
Je suis en 1ère S et on vient tout juste de finir les suites
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
par Xeniuss » 20 Avr 2012, 00:49
maths0 a écrit: Comment trouves-tu la même chose avec wn ?
Cela voudrait dire que:
alors que c'est en vrai
Tu as vérifié le calcul de wn que tu as fait ? ?
Bah j'ai développé l'expression tout simplement sans calculer les termes suivant
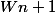
et je tombe sur
et après j'ai calculer les 3 premier termes pour essayer de faire la somme et sa a l'air bon
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
par maths0 » 20 Avr 2012, 00:50
Tu t'es trompé dans ton calcul de wn.
.
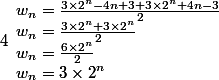
Soit tu identifies a partir de là.
Ou alors finalement (il faut d'ailleurs toujours faire cela quand on ne reconnait pas):
 + 3}}{2} + \frac{{3 \times {2^{n + 1}} + 4\left( {n + 1} \right) - 3}}{2}\\<br />{w_{n + 1}} = \frac{{3 \times {2^n} \times 2 - 4\left( {n + 1} \right) + 3}}{2} + \frac{{3 \times {2^n} \times 2 + 4\left( {n + 1} \right) - 3}}{2}\\<br />{w_{n + 1}} = \frac{{6 \times {2^n} - 4n - 4 + 3 + 6 \times {2^n} + 4n + 4 - 3}}{2}\\<br />{w_{n + 1}} = \frac{{12 \times {2^n}}}{2}\\<br />{w_{n + 1}} = 6 \times {2^n}\\<br />{w_{n + 1}} = 2{w_n}<br />\end{array})
Donc
)
est une suite géométrique de raison q=2 et de premier terme
.
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
par Xeniuss » 20 Avr 2012, 00:55
maths0 a écrit:Tu t'es trompé dans ton calcul de wn.
.
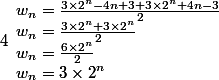
Soit tu identifies a partir de là.
Ou alors finalement (il faut d'ailleurs toujours faire cela quand on ne reconnait pas):
Donc
est une suite géométrique de raison q=2 et de premier terme
.
Oui voila j'était en train de l'écrire mais j'suis pas habitué a écrire les calcul sur ordi :p
Merci beaucoup!
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
par Xeniuss » 20 Avr 2012, 00:58
Dans ce cas je ne suis pas obligé de faire le calcul avec Wn+1??
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
par maths0 » 20 Avr 2012, 01:00
Comme tu veux.
Je me relis ça semble faut, soit moi soit toi.
 + 3}}{2} - \frac{{3 \times {2^{n + 1}} + 4\left( {n + 1} \right) - 3}}{2}\\<br />{t_{n + 1}} = \frac{{3 \times {2^n} \times 2 - 4\left( {n + 1} \right) + 3}}{2} - \frac{{3 \times {2^n} \times 2 + 4\left( {n + 1} \right) - 3}}{2}\\<br />{t_{n + 1}} = \frac{{3 \times {2^n} \times 2 - 4\left( {n + 1} \right) + 3 - \left( {3 \times {2^n} \times 2 + 4\left( {n + 1} \right) - 3} \right)}}{2}\\<br />{t_{n + 1}} = \frac{{6 \times {2^n} - 4\left( {n + 1} \right) + 3 - 6 \times {2^n} - 4n - 4 + 3}}{2}\\<br />{t_{n + 1}} = \frac{{ - 8n - 2}}{2}\\<br />{t_{n + 1}} = - 4n - 1<br />\end{array})
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
par maths0 » 20 Avr 2012, 01:06
J'ai fais une erreur (pas de lien entre t(n+1) et t(n) ), je la recherche... si tu vois sur le post du dessus.
}}{2}\\ {t_n} = \frac{{3 \times {2^n} - 4n + 3 - 3 \times {2^n} - 4n + 3}}{2}\\ {t_n} = \frac{{ - 8n + 6}}{2}\\ {t_n} = - 4n + 3 \end{array})
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
par Xeniuss » 20 Avr 2012, 01:07
je re calcul de mon côté pour voir :)
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
par maths0 » 20 Avr 2012, 01:14
C'est bon finalement:
.
J'étais resté sur les suites géométriques :s
Donc:
)
est une suite arithmétique de raison r=-4 et de premier terme
.
Finalement:
et
.
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
par Xeniuss » 20 Avr 2012, 01:15
maths0 a écrit:J'ai fais une erreur (pas de lien entre t(n+1) et t(n) ), je la recherche... si tu vois sur le post du dessus.
Ha oui moi je n'ai simplifié que le 8 parce qu'on ma dit que l'on pouvait pas tout simplifier je m'explique par le calcul
or on peut l'écrire
et donc le 2 en dénominateur ne peut annuler qu'un seul 2 du nominateur je me trompe?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
par maths0 » 20 Avr 2012, 01:24
Si tu as des questions n'hésite pas. Il faut s'organiser.
Maintenant le 3) quand est-ce qu'une suite est constante ?
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
par Xeniuss » 20 Avr 2012, 01:26
Heu la 3) de l'exercice 1?
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
par maths0 » 20 Avr 2012, 01:28
Nous sommes à l'exercice 2.
J'ai dis n'importe quoi au dessus alors ...
Tu as réussi à prouver l'égalité ?
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
par Xeniuss » 20 Avr 2012, 01:28
Une suite est constante quand tout ses réel sont les même Un+1= Un je me trompe? :o
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
par Xeniuss » 20 Avr 2012, 01:29
maths0 a écrit:Nous sommes à l'exercice 2.
J'ai dis n'importe quoi au dessus alors ...
Tu as réussi à prouver l'égalité ?
La suite constante c'est dans l'exercice 1 :p mais je n'y arrive pas nn plus :/
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 111 invités
