Bonjour,
J'ai un exercice que je parviens pas à résoudre, pouvez vous m'aider svp?
Alors, j'ai une suite (Vn) géométrique de raison 1/6 et de premier terme V0=4.
J'ai donc, Vn= V0x q^n = 4x(1/6)^n
De plus, Vn = (Un-4)/(Un+1)
Je trouve alors que Un = (Vn+4)/(-Vn+1)
Cependant je dois ensuite trouver Un en fonction de n, donc Un=(4x(1/6)^n + 4)/(-4x(1/6)^n + (1/4)).
En factorisant par 4, j'obtiens Un= ((1/6)^n +1)/(-1x(1/6)^n+(1/4))
J'aimerais savoir tout d'abord si mon calcul est juste, si je peux le développer d'avantage ?
Enfin, si je ne peux pas développer plus, pouvez vous m'aider à trouver la limite de Un car je n'y parviens pas..
Merci beaucoup.
Suites et étude de fonction
9 messages
- Page 1 sur 1
Bonjour,
Je trouve aussi que Un = (Vn+4)/(-Vn+1) mais je préfère l'exprimer sous la forme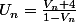
Par contre, je crois qu'il n'y a pas d'erreur dans le calculde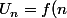) .
.
J'ai envisagé séparément le numératuer et de dénominateur de U_n et obtient donc une expression un peu diffèrente:
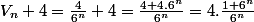
et
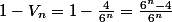
d'où
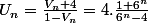
Pour les limites:
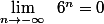 d'où
d'où 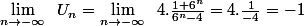
Par contre pour la limite en , il est plus facile de factoriser par
, il est plus facile de factoriser par  :
:
}{6^n.(1+\frac4{6^n}}\\<br />U_n = 4.\frac{\frac1{6^n}+1}{1+\frac4{6^n}}\\<br />U_n = 4.\frac{\frac1{6^n}+1}{1+4.\frac1{6^n}}\\)
Ce qui est bien l'expression donnée par algo1308
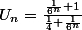
Or,
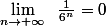 d'où
d'où 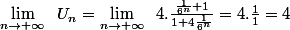
Ou de façon équivalente :
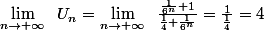
Je trouve aussi que Un = (Vn+4)/(-Vn+1) mais je préfère l'exprimer sous la forme
Par contre, je crois qu'il n'y a pas d'erreur dans le calculde
J'ai envisagé séparément le numératuer et de dénominateur de U_n et obtient donc une expression un peu diffèrente:
et
d'où
Pour les limites:
Par contre pour la limite en
Ce qui est bien l'expression donnée par algo1308
Or,
Ou de façon équivalente :
Merci beaucoup, mais je ne comprend comment vous avez trouver Un car je suis d'accord que c'est Un = (Vn+4)/(-Vn+1), je suis d'accord pour le calcul du dénominateur et du numérateur séparément mais je ne comprend pas quand vous les avez rassemblé comment vous avez obtenu : Un= 4 * ((1+6^n)/(6^n-4))
De plus, quelle expression de Vn dois-je utiliser afin de trouver la limite de vn ?
De plus, quelle expression de Vn dois-je utiliser afin de trouver la limite de vn ?
En rassemblant le numérateur et dénominateur, je fais simplement disparaitre 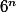 .
.
Concernant les formules à utiliser,cela dépent de la limite considérée.
Ma formule permet de calculer directemetn la limite pour n tendant vers -oo car dans ce cas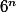 s'annule et on voit apparaitre la valeur limite en -oo.
s'annule et on voit apparaitre la valeur limite en -oo.
Par contre en , votre formule est plus efficace car les
, votre formule est plus efficace car les  s'annulent ce qui laisse apparaitre la valeur limite en +oo.
s'annulent ce qui laisse apparaitre la valeur limite en +oo.
Concernant les formules à utiliser,cela dépent de la limite considérée.
Ma formule permet de calculer directemetn la limite pour n tendant vers -oo car dans ce cas
Par contre en
Ah d'accord j'ai compris merci !!!
Mais donc pour la limite de Un je suis d'accord. Par contre on me demande de calculer celle de Vn. Comment dois-je faire ? Je dois m'aider de Vn=4*1/6^n ou de Vn = (Un-4)/(Un+1).
Car si jutilise la premiere expression de Vn, j'ai lim 4* 1/6^n quand n tend vers plus ou moins l'infini je ne sais pas ce que ça vaut...
Mais donc pour la limite de Un je suis d'accord. Par contre on me demande de calculer celle de Vn. Comment dois-je faire ? Je dois m'aider de Vn=4*1/6^n ou de Vn = (Un-4)/(Un+1).
Car si jutilise la premiere expression de Vn, j'ai lim 4* 1/6^n quand n tend vers plus ou moins l'infini je ne sais pas ce que ça vaut...
En fait non ce n'est pas faux, on peux utiliser directemetn l'expression de V_n ou utiliser les résultats obtenus pour U_n.
On obtient bien les mêmes résultats :
Si on considère :
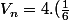^n = 4.\frac1{6^n})
Sachant que , on a
, on a 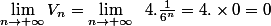
Si on considère :

Sachant que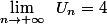 on a,
on a, 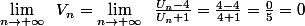
On peut faire de même pour la limite en -oo
Vérifons numériquement à la calculette :
On constate que la valeur limite est rapidement atteinte !
On obtient bien les mêmes résultats :
Si on considère :
Sachant que
Si on considère :
Sachant que
On peut faire de même pour la limite en -oo
Vérifons numériquement à la calculette :
- Code: Tout sélectionner
n Vn Un
0 4.0000 -2.6667
1 0.6667 14.0000
2 0.1111 4.6250
3 0.0185 4.0943
4 0.0031 4.0155
5 0.0005 4.0026
6 0.0001 4.0004
7 0.0000 4.0001
8 0.0000 4.0000
On constate que la valeur limite est rapidement atteinte !
@C.Ret
Bravo pour tes explications
Ce message est juste pour réagir à ta conclusion aux tests que tu as simulé sur une calculatrice
pour éviter qu'ils ne soient mal interprétés...
je tenais à préciser que
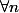
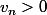
et que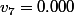 est l'affichage sur la calculatrice de
est l'affichage sur la calculatrice de 
Info supplémentaires :
Pour les suites convergentes , on peut étudier la vitesse de convergence de ces suites et on peut les classifier sous 3 catégories
1) suites dont la convergence est lente ( exemple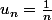 )
)
2) suites dont la convergence est linéaire (exemple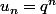 avec |q| 1 )
avec |q| 1 )
Commentaire surprenant
la suite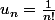 est la plus LENTE des SUITES RAPIDES
est la plus LENTE des SUITES RAPIDES
A+
Bravo pour tes explications
Ce message est juste pour réagir à ta conclusion aux tests que tu as simulé sur une calculatrice
pour éviter qu'ils ne soient mal interprétés...
C.Ret a écrit:Vérifons numériquement à la calculette :
- Code: Tout sélectionner
n Vn Un
0 4.0000 -2.6667
1 0.6667 14.0000
2 0.1111 4.6250
3 0.0185 4.0943
4 0.0031 4.0155
5 0.0005 4.0026
6 0.0001 4.0004
7 0.0000 4.0001
8 0.0000 4.0000
On constate que la valeur limite est rapidement atteinte !
je tenais à préciser que
et que
Info supplémentaires :
Pour les suites convergentes , on peut étudier la vitesse de convergence de ces suites et on peut les classifier sous 3 catégories
1) suites dont la convergence est lente ( exemple
2) suites dont la convergence est linéaire (exemple
Commentaire surprenant
la suite
A+
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
